
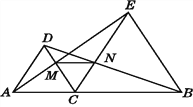
【题目】如图,点C是线段AB上任意一点(点C与点A,B不重合),分别以AC,BC为边在直线AB的同侧作等边三角形ACD和等边三角形BCE,AE与CD相交于点M,BD与CE相交于点N.连接MN.
试说明:(1)△ACM≌△DCN;(2)MN∥AB.
【答案】见解析
【解析】试题分析: ![]() 由已知条件可利用两边及其夹角相等的三角形全等得△ACE≌△DCB. 由全等三角形的性质可得∠CAE=∠CDB,接下来根据两角及其夹边相等的三角形全等即可得到结论;
由已知条件可利用两边及其夹角相等的三角形全等得△ACE≌△DCB. 由全等三角形的性质可得∠CAE=∠CDB,接下来根据两角及其夹边相等的三角形全等即可得到结论;
![]() 证明第一问的方法类似,可证得△BCN≌△ECM,进而可以得出△CMN是等边三角形,
证明第一问的方法类似,可证得△BCN≌△ECM,进而可以得出△CMN是等边三角形,
试题解析:(1)∵ △ACD、△BCE为等边三角形,
![]()
![]()
![]()
∴ △ACE≌△DCB.
∴ ∠CAE=∠CDB,
∵ ∠DCA=∠BCE=60°,
∴ ∠DCE=60°,
∵ ∠CAE=∠CDB,AC=CD,∠ACD=∠DCE,
∴ △ACM≌△DCN.
(2)∵ △ACE≌△BCD,
∴ ∠MEC=∠NBC,
∵ ∠BCE=∠ECM=60°,BC=CE,∠MEC=∠NBC,
∴ △BCN≌△ECM,
∴ CM=CN,
∵ CM=CN,∠ECM=60°,
∴ △CMN是等边三角形,
∴ ∠MNC=60°,
∵ ∠BCE=∠MNC=60°,
∴ MN∥AB.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,已知AD∥BC,∠1=∠2,要说明∠3+∠4=180°,请补充完整解题过程,并在括号内填上相应的依据:

解:因为AD∥BC(已知),
所以∠1=∠3(___________).
因为∠1=∠2(已知),
所以∠2=∠3.
所以BE∥___________ (___________).
所以∠3+∠4=180°(___________).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】6月5日是世界环境日,为了普及环保知识,增强环保意识,某市第一中学举行了“环保知识竞赛”,参赛人数1000人,为了了解本次竞赛的成绩情况,学校团委从中抽取部分学生的成绩(满分为100分,得分取整数)进行统计,并绘制出不完整的频率分布表和不完整的频数分布直方图如下:

(1)直接写出a的值,并补全频数分布直方图.
分组 | 频数 | 频率 |
49.5~59.5 | 0.08 | |
59.5~69.5 | 0.12 | |
69.5~79.5 | 20 | |
79.5~89.5 | 32 | |
89.5~100.5 | a |
(2)若成绩在80分以上(含80分)为优秀,求这次参赛的学生中成绩为优秀的约为多少人?
(3)若这组被抽查的学生成绩的中位数是80分,请直接写出被抽查的学生中得分为80分的至少有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,点A(3,4),B(5,0),C(0,﹣2).在第一象限找一点D,使四边形AOBD成为平行四边形,
(1)点D的坐标是;
(2)连接OD,线段OD、AB的关系是;
(3)若点P在线段OD上,且使PC+PB最小,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
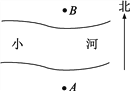
【题目】如图所示的A、B是两根呈南北方向排列的电线杆,A、B之间有一条小河,小刚想估测这两根电线杆之间的距离,于是小刚从A点开始向正西方向走了20步到达一棵大树C处,接着又向前走了20步到达D处,然后他左转90°直行,当他看到电线杆B、大树C和他自己现在所处的位置E恰在同一条直线上时,他从D位置走到E处恰好走了100步,利用上述数据,小刚测出了A、B两根电线杆之间的距离.
(1)请你根据上述的测量方法在原图上画出示意图;
(2)如果小刚一步大约60厘米,请你求A、B两根电线杆之间的距离并简述理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ADF≌△CBE,且点E,B,D,F在一条直线上.试判断:
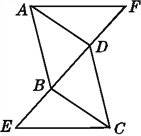
(1)AD与BC的位置关系(并加以说明);
(2)BF与DE的数量关系,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com