
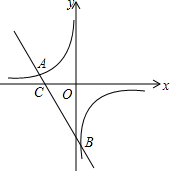
 如图所示,直线y=-2x+b与反比例函数$y=\frac{k}{x}$交于点A、B,与x轴交于点C.
如图所示,直线y=-2x+b与反比例函数$y=\frac{k}{x}$交于点A、B,与x轴交于点C.分析 (1)不等式的解即为函数y=-2x+b的图象在函数y=$\frac{k}{x}$上方的x的取值范围.可由图象直接得到.
(2)用b表示出OC和OF的长度,求出∠OCF的正切值,进而求出sin∠OCB.
解答 解:(1)如图,由图象可知不等式$-2x+b>\frac{k}{x}$的解是x<-3或0<x<1;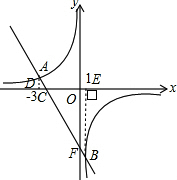
(2)设直线AB与y轴的交点为F.
当y=0时,$x=\frac{b}{2}$,即$OC=-\frac{b}{2}$,
当x=0时,y=b,即OF=-b,
∵直线y=-2x+b的斜率为-2,
∴tan∠OCB=$\frac{OF}{OC}$=2,
∴OF=2OC,
∴AB=$\sqrt{O{F}^{2}+O{C}^{2}}$=$\sqrt{5}$OC,
∴sin∠OCB=$\frac{2OC}{\sqrt{5}OC}$=$\frac{2\sqrt{5}}{5}$.
点评 这道题主要考查反比例函数的图象与一次函数的交点问题,借助图象分析之间的关系,体现数形结合思想的重要性.


科目:初中数学 来源: 题型:填空题
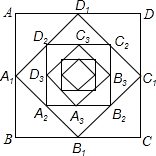 如图,在边长为2的正方形ABCD中,顺次连接各边中点得正方形A1B1C1D1,又依次连接正方形A1B1C1D1各边中点得正方形A2B2C2D2,以此规律已知作下去,那么正方形A8B8C8D8的周长是$\frac{1}{2}$.
如图,在边长为2的正方形ABCD中,顺次连接各边中点得正方形A1B1C1D1,又依次连接正方形A1B1C1D1各边中点得正方形A2B2C2D2,以此规律已知作下去,那么正方形A8B8C8D8的周长是$\frac{1}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,抛物线y=x2+bx+c与x轴交于A(-2,0),B(6,0)两点.
如图,抛物线y=x2+bx+c与x轴交于A(-2,0),B(6,0)两点.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
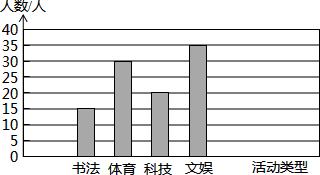 某校对初中学生开展的四项课外活动进行了一次抽样调查(每人只参加其中的一项活动),调查结果如图所示.根据图示所提供的样本数据,可得学生参加体育活动的频率是0.3.
某校对初中学生开展的四项课外活动进行了一次抽样调查(每人只参加其中的一项活动),调查结果如图所示.根据图示所提供的样本数据,可得学生参加体育活动的频率是0.3.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com