
 如图,圆柱形水管内原有积水的水平面宽CD=20cm,水深GF=2cm,若水面上升2cm(即EG=2cm),则此时水面宽AB为( )
如图,圆柱形水管内原有积水的水平面宽CD=20cm,水深GF=2cm,若水面上升2cm(即EG=2cm),则此时水面宽AB为( )| A. | 8$\sqrt{3}$cm | B. | 16$\sqrt{3}$cm | C. | 8cm | D. | 16cm |
分析 连接OA、OC.设⊙O的半径是R,则OG=R-2,OE=R-4.根据垂径定理,得CG=10.在直角三角形OCG中,根据勾股定理求得R的值,再进一步在直角三角形OAE中,根据勾股定理求得AE的长,从而再根据垂径定理即可求得AB的长.
解答 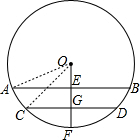 解:如图所示,连接OA、OC.
解:如图所示,连接OA、OC.
设⊙O的半径是R,则OG=R-2,OE=R-4.
∵OF⊥CD,
∴CG=$\frac{1}{2}$CD=10cm.
在直角三角形COG中,根据勾股定理,得
R2=102+(R-2)2,
解,得R=26.
在直角三角形AOE中,根据勾股定理,得
AE=$\sqrt{2{6}^{2}-2{2}^{2}}$=8$\sqrt{3}$cm.
根据垂径定理,得AB=16$\sqrt{3}$(cm),
故选B.
点评 本题考查了勾股定理,垂径定理的应用,能构造直角三角形是解此题的关键,注意:垂直于弦的直径平分弦.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | -$\frac{1}{3}$ | C. | 0 | D. | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 129名 | B. | 120名 | C. | 108名 | D. | 96名 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -$\frac{8}{5}$ | B. | $\frac{8}{5}$ | C. | -$\frac{4}{5}$ | D. | $\frac{4}{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com