
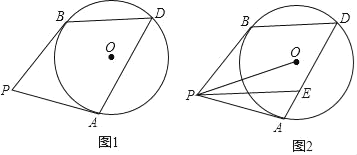
【题目】如图,PA、PB是⊙O的切线,A,B为切点,D为⊙O上一点.
(1)求证:∠P=180°﹣2∠D;
(2)如图,PE∥BD交AD于点E,若DE=2AE,tan∠OPE=![]() ,⊙O的半径为2
,⊙O的半径为2![]() ,求AE的长.
,求AE的长.
【答案】(1)证明见解析;(2)4
【解析】
(1)连接OA,OB,由PA,PB为⊙O的切线,根据切线的性质,即可得∠OAP=∠OBP=90°,又由圆周角定理,可求得∠AOB=2∠D,继而可求得结论.
(2)过点O作OG⊥AD,连接OB,OE,连接OA交PE于点F,由PE∥BD,可得△OPF∽△EFA,即可求得∠OPE=∠OAD,从而可求得AG,即可求出AE
(1)证明:如图1,连接OA,OB,
∵PA,PB为⊙O的切线,
∴∠OAP=∠OBP=90°,
∴∠P=360°﹣90°﹣90°﹣∠AOB=180°﹣∠AOB,
∵∠AOB=2∠D,
∴∠P=180°﹣2∠D;
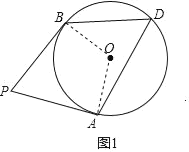
(2)
如图2,过点O作OG⊥AD,连接OB,OE,连接OA交PE于点F
由(1)得,∠OPA=90°﹣∠D
OB⊥PB;OA⊥PA
∴∠POA=180°﹣90°﹣∠OPA=∠D
又∵PE∥BD,
∴∠D=∠PEA
∴∠PEA=∠POA
∵∠PFO=∠EFA
∴△OPF∽△EFA
∴∠OPE=∠OAD
∴tan∠OAD=tan∠OPE=![]()
∴OG=![]() AG
AG
∴在△OAG中,由勾股定理得
AG2+OG2=OA2![]() ,解得AG=6
,解得AG=6
∴AD=12
又∵DE=2AE
∴AE=![]() AD=
AD=![]() ×12=4
×12=4



 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案科目:初中数学 来源: 题型:
【题目】某校为了解全校![]() 名学生到校上学的方式,在全校随机抽取了若干名学生进行问卷调查,问卷给出了五种上学方式供学生选择,每人必选一项,且只能选一项.请根据下面两个不完整的统计图回答以下问题:
名学生到校上学的方式,在全校随机抽取了若干名学生进行问卷调查,问卷给出了五种上学方式供学生选择,每人必选一项,且只能选一项.请根据下面两个不完整的统计图回答以下问题:

(1)在这次调查中,共抽取了多少名学生;
(2)补全两个统计图;
(3)估计全校所有学生中有多少人乘坐公交车上学.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店购进一批成本为每件30元的商品,商店按单价不低于成本价,且不高于50元销售.经调查发现,该商品每天的销售量y(件)与销售单价x(元)之间满足一次函数关系,其图象如图所示.
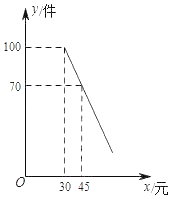
(1)求该商品每天的销售量y(件)与销售单价x(元)之间的函数关系式;
(2)销售单价定为多少元时,才能使销售该商品每天获得的利润w(元)最大?最大利润是多少?
(3)若商店要使销售该商品每天获得的利润高于800元,请直接写出每天的销售量y(件)的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】反比例函数![]() 在第一象限的图象如图所示,过点A(1,0)作x轴的垂线,交反比例函数
在第一象限的图象如图所示,过点A(1,0)作x轴的垂线,交反比例函数![]() 的图象于点M,△AOM的面积为3.
的图象于点M,△AOM的面积为3.

(1)求反比例函数的解析式;
(2)设点B的坐标为(t,0),其中t>1.若以AB为一边的正方形有一个顶点在反比例函数![]() 的图象上,求t的值.
的图象上,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
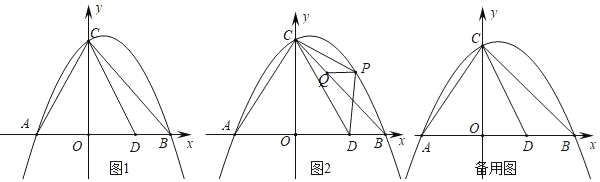
【题目】如图1,抛物线与y=﹣![]() 与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,连接AC、BC,点D是线段AB上一点,且AD=CA,连接CD.
与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,连接AC、BC,点D是线段AB上一点,且AD=CA,连接CD.
(1)如图2,点P是直线BC上方抛物线上的一动点,在线段BC上有一动点Q,连接PC、PD、PQ,当△PCD面积最大时,求PQ+![]() CQ的最小值;
CQ的最小值;
(2)将过点D的直线绕点D旋转,设旋转中的直线l分别与直线AC、直线CO交于点M、N,当△CMN为等腰三角形时,直接写出CM的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有4张看上去无差别的卡片,上面分别写着1,2,3,4.
(1)一次性随机抽取2张卡片,求这两张卡片上的数字之和为奇数的概率;
(2)随机摸取1张后,放回并混在一起,再随机抽取1张,求两次取出的卡片上的数字之和等于4的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果批发商销售每箱进价为40元的柑橘,物价部门规定每箱售价不得高于55元;市场调查发现,若每箱以45元的价格销售,平均每天销售105箱;每箱以50元的价格销售,平均每天销售90箱.假定每天销售量y(箱)与销售价x(元/箱)之间满足一次函数关系式.
(1)求平均每天销售量y(箱)与销售价x(元/箱)之间的函数关系式;
(2)求该批发商平均每天的销售利润w(元)与销售价x(元/箱)之间的函数关系式;
(3)当每箱苹果的销售价为多少元时,可以获得最大利润?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明想测量一棵树的高度,他发现树的影子恰好落在地面和一斜坡上;如图,此时测得地面上的影长为8米,坡面上的影长为4米.已知斜坡的坡角为300,同一时 刻,一根长为l米、垂直于地面放置的标杆在地面上的影长为2米,则树的高度为【 】
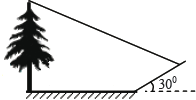
A.![]() 米 B.12米 C.
米 B.12米 C.![]() 米 D.10米
米 D.10米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:点A与⊙O上所有点的连线段中,长度的最小值称为点A到⊙O的最小距离,记为mA;点A与⊙O上所有点的连线段中,长度的最大值称为点A到⊙O的最大距离,记为MA,如图,⊙O的半径为r,点A在⊙O外,且OA=d,则mA=d﹣r.证明如下:
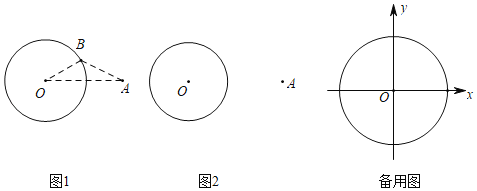
证明:如图1,设B为圆上任意一点,连结OA、OB、AB
①当O、A、B不共线时,AB>OA﹣OB
即AB>d﹣r
②当O、A、B共线时,AB=OA﹣OB
即AB=d﹣r
综上,AB≥d﹣r,即mA=d﹣r
(1)利用刚才的证明,结合所给的图2,⊙O的半径为r,点A在⊙O外,且OA=d,探究MA,你的结论是MA= ,请证明你的结论;
(2)已知⊙O的半径为2,mA=4,则MA= ;
(3)在平面直角坐标系中,以原点O为圆心,6为半径作⊙O,第二象限的点A的坐标为(﹣3,a),且mA=1,求a的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com