
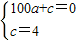
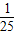 ,c=4,
,c=4, x2+4.
x2+4.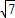 ,此时水面宽度EF=4
,此时水面宽度EF=4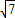 米.
米.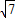 <2.7,
<2.7,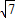 ≈2.65,4
≈2.65,4 ≈10.6
≈10.6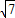 -10≈0.6.(8分)
-10≈0.6.(8分)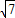 =
=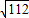 在10到11之间,
在10到11之间,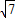 =
= <10.6,
<10.6,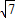 -10<0.6,(8分)
-10<0.6,(8分)

 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源:第3章《圆》中考题集(17):3.1 圆(解析版) 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2005年全国中考数学试题汇编《圆》(12)(解析版) 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2005年广东省佛山市中考数学试卷(课标卷)(解析版) 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2011年浙江省九年级下学期第三次月考数学卷 题型:选择题
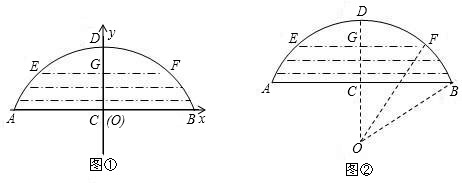
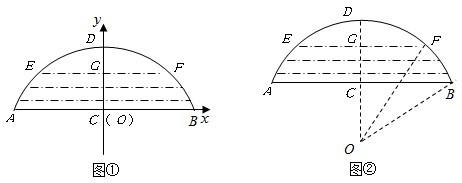
一座拱型桥,桥下水面宽度AB是20米,拱高CD是4米.若水面上升3米至EF,则水面宽度EF是多少?
1.若把它看作是抛物线的一部分,在坐标系中(如图1)可设抛物线的表达式为 .
.
请你填空:a= ,c= ,EF= 米.
2.若把它看作是圆的一部分,则可构造图形(如图2)计算如下:
设圆的半径是r米,在Rt△OCB中,易知 ,r=14.5
,r=14.5
同理,当水面上升3米至EF,在Rt△OGF中可计算出GF= 米,即水面宽度EF= 米.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com