
【题目】如图,四边形ABCD和四边形AEFG均为菱形,且∠EAG=∠ABC.
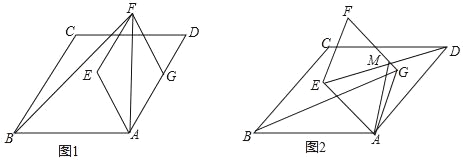
(1)如图1,点G在线段AD上,已知AD=5,AG=3,且cos∠ABC=![]()
![]() ,连接AF,BF,求BF的长;
,连接AF,BF,求BF的长;
(2)如图2,点G在菱形ABCD内部,连接BG、DE,若点M为DE中点,试猜想AM与BG之间的数量关系,并证明你的结论.
【答案】(1)BF=![]() ;(2)BG=2AM,见解析.
;(2)BG=2AM,见解析.
【解析】
(1)由cos∠ABC=![]() 得到∠EAG=∠ABC=60°,由AF为菱形对角线得到AF平分∠EAG,求得∠BAF=90°.已知AB=AD=5,所以在Rt△ABF中只要求出AF即能求出BF.又因为AF为菱形对角线且已知菱形边长为3,连接另一对角线EG,根据对角线互相垂直平分且∠FAG=30°即能求出BF.
得到∠EAG=∠ABC=60°,由AF为菱形对角线得到AF平分∠EAG,求得∠BAF=90°.已知AB=AD=5,所以在Rt△ABF中只要求出AF即能求出BF.又因为AF为菱形对角线且已知菱形边长为3,连接另一对角线EG,根据对角线互相垂直平分且∠FAG=30°即能求出BF.
(2)图形比较复杂,关键条件为∠EAG=∠ABC的运用.因为菱形中∠ABC与∠BAD互补,则∠ABC与∠BAD的补角相等,延长BA构造∠DAH=∠ABC,所以∠EAG=∠DAH,中间加上公共角∠DAG,易得∠EAD=∠GAH且EA=GA,所以使BA的延长线AH=AD即能构造出△ADE≌△AHG.取GH中点P,则AM、AP为全等三角形对应中线,AM=AP,问题转化为AP与BG的数量关系.又A、P分别为BH、GH中点,根据中位线定理,BG=2AP,得证.
解:(1)连接EG,交AF于点O,(如图1)
∵四边形AEFG为菱形
∴EG⊥AF,AF=2OA,AF平分∠EAG
∵cos∠ABC=![]() ,
,
∴∠EAG=∠ABC=60°
∴∠OAG=![]() ∠EAG=30°
∠EAG=30°
∵AG=3,∠AOG=90°
∴OG=![]() AG=
AG=![]()
∴OA=![]() =
=![]()
∴AF=2OA=![]()
∵菱形ABCD中,∠ABC=60°,AD∥BC,AB=5
∴∠BAD=180°﹣∠ABC=120°,AD=AB=5
∴∠BAF=∠BAD﹣∠DAF=120°﹣30°=90°
∴BF=![]()
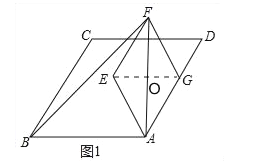
(2)猜想BG=2AM,证明如下:
延长BA至H,使AH=AB,连接GH,取GH中点P,连接AP,(如图2)
∵四边形ABCD和四边形AEFG为菱形
∴AD=AB=AH,AE=AG,BC∥AD
∴∠ABC=∠HAD
∵∠EAG=∠ABC
∴∠EAG=∠HAD
∴∠EAG+∠DAG=∠
即∠EAD=∠GAH
在△ADE与△AHG中
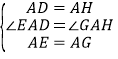 ,
,
∴△ADE≌△AHG(SAS)
∵M是DE中点,P是GH中点,即AM与AP为全等三角形对应中线
∴AM=AP
∵A为BH中点,
∴AP为△BGH中位线
∴BG=2AP
∴BG=2AM


科目:初中数学 来源: 题型:
【题目】如图,点A在数轴上对应的数为20,以原点O为圆心,OA为半径作优弧![]() ,使点B在O右下方,且tan∠AOB=
,使点B在O右下方,且tan∠AOB=![]() ,在优弧
,在优弧![]() 上任取一点P,且能过P作直线l∥OB交数轴于点Q,设Q在数轴上对应的数为x,连接OP.
上任取一点P,且能过P作直线l∥OB交数轴于点Q,设Q在数轴上对应的数为x,连接OP.
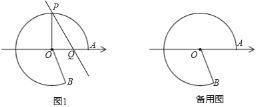
(1)若优弧上一段![]() 的长为10π,求∠AOP度数及x的值.
的长为10π,求∠AOP度数及x的值.
(2)若线段PQ的长为10,求这时x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知矩形PMON的边OM、ON分别在x、y轴上,O为坐标原点,且点P的坐标为(﹣2,3).将矩形PMON沿x轴正方向平移4个单位,得到矩形P1M1O1N1再将矩形P1M1O1N1绕着点O1旋转90°得到矩形P2M2O2N2.在坐标系中画出矩形P2M2O2N2,并求出直线P1P2的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
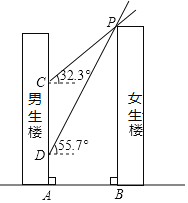
【题目】如图,男生楼在女生楼的左侧,两楼高度均为90m,楼间距为AB,冬至日正午,太阳光线与水平面所成的角为![]() ,女生楼在男生楼墙面上的影高为CA;春分日正午,太阳光线与水平面所成的角为
,女生楼在男生楼墙面上的影高为CA;春分日正午,太阳光线与水平面所成的角为![]() ,女生楼在男生楼墙面上的影高为DA,已知
,女生楼在男生楼墙面上的影高为DA,已知![]() .
.
![]() 求楼间距AB;
求楼间距AB;
![]() 若男生楼共30层,层高均为3m,请通过计算说明多少层以下会受到挡光的影响?
若男生楼共30层,层高均为3m,请通过计算说明多少层以下会受到挡光的影响?![]() 参考数据:
参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
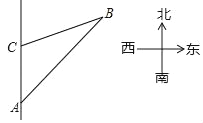
【题目】一艘货轮以36km/h的速度在海面上沿正北方向航行,当行驶至A处时,发现北偏东37°方向有一个灯塔B,货轮继续向北航行20分钟后到达C处,发现灯塔B在它的北偏东67°方向,则此时货轮与灯塔B的距离为_____km.(结果精确到0.1,参考数据:sin37°≈0.6,cos37°≈0.8,tan37°≈0.75,sin67°≈0.920,cos67°≈0.391,tan67°≈2.356)
查看答案和解析>>
科目:初中数学 来源: 题型:
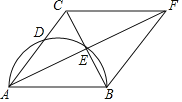
【题目】如图,在![]() 中,
中,![]() ,以AB为直径的圆交AC于点D,交BC于点E,延长AE至点F,使
,以AB为直径的圆交AC于点D,交BC于点E,延长AE至点F,使![]() ,连接FB,FC.
,连接FB,FC.
![]() 求证:四边形ABFC是菱形;
求证:四边形ABFC是菱形;
![]() 若
若![]() ,
,![]() ,求半圆和菱形ABFC的面积.
,求半圆和菱形ABFC的面积.
![]() 只用一把无刻度的直尺,作出菱形AB上的高CH.
只用一把无刻度的直尺,作出菱形AB上的高CH.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=﹣x2+bx+c经过点B(﹣1,0)和点C(2,3).
(1)求此抛物线的函数表达式;
(2)如果此抛物线上下平移后过点(﹣2,﹣1),试确定平移的方向和平移的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某塔观光层的最外沿点E为蹦极项目的起跳点.已知点E离塔的中轴线AB的距离OE为10米,塔高AB为123米(AB垂直地面BC),在地面C处测得点E的仰角α=45°,从点C沿CB方向前行40米到达D点,在D处测得塔尖A的仰角β=60°,求点E离地面的高度EF.(结果精确到0.1米)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com