
【题目】如图所示,△ABC中,A(﹣2,1)、B(﹣4,﹣2)、C(﹣1,﹣3),△A′B′C′是△ABC平移之后得到的图,并且C的对应点C′的坐标为(4,1)。
(1)A′、B′.两点的坐标分别为A′ 、B′ ;
(2)请作出△ABC平移之后的图形△A′B′C′;

(3)求△A′B′C′的面积.
【答案】(1)(3,5),(1,2);(2)见解析;(3)![]() .
.
【解析】
(1)由点C(﹣1,﹣3)平移到C′(4,1)可知,图形的平移规律是:先向右平移5个单位,再向上平移4个单位,根据此规律即可求出A′、B′的坐标;
(2)描出A′、B′、C′三点的坐标,再依次连接即可;
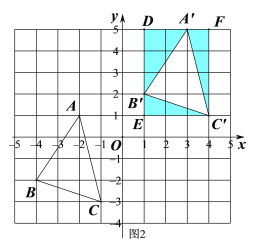
(3)如图2,S△A'B'C'= S矩形C'EDF-S△A'C'F-S△A'B'D-S△B'C'E,再代入数据进行计算即可.
解:(1)由点C(﹣1,﹣3)平移到C′(4,1)可知,图形的平移规律是:先向右平移5个单位,再向上平移4个单位,所以A′、B′的坐标分别是(﹣2+5,1+4)、(﹣4+5,﹣2+4),即A′(3,5)、B′(1,2);
故答案为(3,5),(1,2);
(2)如图1,△A′B′C′即为所求.

(3)如图2,S△A'B'C'= S矩形C'EDF-S△A'C'F-S△A'B'D-S△B'C'E
=![]()
=![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图1和2,在20×20的等距网格(每格的宽和高均是1个单位长)中,Rt△ABC从点A与点M重合的位置开始,以每秒1个单位长的速度先向下平移,当BC边与网的底部重合时,继续同样的速度向右平移,当点C与点P重合时,Rt△ABC停止移动.设运动时间为x秒,△QAC的面积为y.
(1)如图1,当Rt△ABC向下平移到Rt△A1B1C1的位置时,请你在网格中画出Rt△A1B1C1关于直线QN成轴对称的图形;
(2)如图2,在Rt△ABC向下平移的过程中,请你求出y与x的函数关系式,并说明当x分别取何值时,y取得最大值和最小值?最大值和最小值分别是多少?
(3)在Rt△ABC向右平移的过程中,请你说明当x取何值时,y取得最大值和最小值?最大值和最值分别是多少?为什么?(说明:在(3)中,将视你解答方法的创新程度,给予1~4分的加分)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形![]() 中,延长
中,延长![]() 至
至![]() 使
使![]() ,以
,以![]() 为边作正方形
为边作正方形![]() ,延长
,延长![]() 交
交![]() 于
于![]() ,连接
,连接![]() ,
,![]() ,
,![]() 为
为![]() 的中点,连接
的中点,连接![]() 分别与
分别与![]() ,
,![]() 交于点
交于点![]() .则下列说法:①
.则下列说法:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .其中正确的有( )
.其中正确的有( )

A.4个B.3个C.2个D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(-3,0),对称轴为直线x=-1,给出四个结论:①b2>4ac;②2a+b=0;③a+b+c>0;④若点B(-![]() ,y1),C(-
,y1),C(-![]() ,y2)为函数图象上的两点,则y1<y2.其中正确结论是___________.
,y2)为函数图象上的两点,则y1<y2.其中正确结论是___________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正方形ABCD,点M是边BA延长线上的动点(不与点A重合),且AM<AB,△CBE由△DAM平移得到.若过点E作EH⊥AC,H为垂足,则有以下结论:①点M位置变化,使得∠DHC=60°时,2BE=DM;②无论点M运动到何处,都有DM=![]() HM;③无论点M运动到何处,∠CHM一定大于135°.其中正确结论的序号为_____.
HM;③无论点M运动到何处,∠CHM一定大于135°.其中正确结论的序号为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,AB=8,点E、F分别在AD和AB上,AE=3,AF=4.



(1)点P在边BC上运动、四边形EFPH是平行四边形,连接DH.
①当四边形FPHE是菱形时,线段BP=_____;
②当点P在边BC上运动时,△DEH的面积会不会变化?若变化,求其最大值;若不变,求出它的值;
③当△DEH是等腰三角形时,求BP的长;
(2)若点E沿E-D-C向终点C运动,点F沿F-B-C终点C运动,速度分别为每秒3个单位长度和每秒4个单位长度,当其中一个点到达终点C时,另一个点也停止运动,求EF的中点O的运动路径长(要求写出简略的计算过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2008年5月12日,汶川发生了里氏8.0级地震,给当地人民造成了巨大的损失.某中学全体师生积极捐款,其中九年级的3个班学生的捐款金额如下表:

老师统计时不小心把墨水滴到了其中两个班级的捐款金额上,但他知道下面三条信息:
信息一:这三个班的捐款总金额是7700元;
信息二:二班的捐款金额比三班的捐款金额多300元;
信息三:一班学生平均每人捐款的金额大于48元,小于51元.
请根据以上信息,帮助老师解决:
(1)二班与三班的捐款金额各是多少元?
(2)一班的学生人数是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在 Rt△ABC 中,AB=AC,∠BAC=90°,直线 AE 是经过点A 的任一直线,且与直线 BC 交于点 P(异于点 B、C),BD⊥AE,垂足为 D,CE⊥AE,垂足为 E.试问:
(1)AD 与 CE 的大小关系如何?请说明理由.
(2)写出线段 DE、BD、CE 的数量关系.(直接写出结果,不需要写过程.)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com