
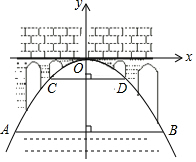
 如图,有一座抛物线型拱桥,桥下面在正常水位AB时宽20米,水位上升3米就达到警戒线CD,这时水面宽度为10米.若洪水到来时,水位以每小时0.2米的速度上升从警戒线开始,再持续多少小时才能到拱桥顶?(平面直角坐标系是以桥顶点为点O的)
如图,有一座抛物线型拱桥,桥下面在正常水位AB时宽20米,水位上升3米就达到警戒线CD,这时水面宽度为10米.若洪水到来时,水位以每小时0.2米的速度上升从警戒线开始,再持续多少小时才能到拱桥顶?(平面直角坐标系是以桥顶点为点O的) 分析 先设抛物线的解析式为y=ax2,再找出几个点的坐标,代入解析式后可求得抛物线的解析式,把b=-1代入即可求出CD的长度,进而求出时间.
解答 解:设所求抛物线的解析式为:
y=ax2.
设D(5,b),则B(10,b-3),
把D、B的坐标分别代入y=ax2得:$\left\{\begin{array}{l}{25a=b}\\{100a=b-3}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=-\frac{1}{25}}\\{b=-1}\end{array}\right.$,
∴y=-$\frac{1}{25}$x2;
∵b=-1,
∴拱桥顶O到CD的距离为1,$\frac{1}{0.2}$=5小时.
所以再持续5小时到达拱桥顶5小时.
点评 本题考查点的坐标的求法及二次函数的实际应用.借助二次函数解决实际问题是解题的关键.


 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案科目:初中数学 来源: 题型:解答题
 已知抛物线y=$\frac{1}{2}$x2-2x-1
已知抛物线y=$\frac{1}{2}$x2-2x-1查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
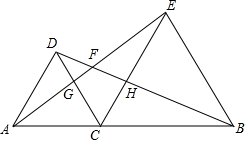 已知:如图,C是线段AB上一点,分别以AC.BC为边作等边△DAC和等边△ECB,AE与BD.CD相交于点F、G,CE与BD相交于点H.
已知:如图,C是线段AB上一点,分别以AC.BC为边作等边△DAC和等边△ECB,AE与BD.CD相交于点F、G,CE与BD相交于点H.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
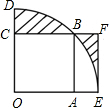 如图:扇形DOE的圆心角为直角,它的半径为2cm,正方形OABC内接于扇形,点A、B、C分别在OE、$\widehat{DE}$、OD上,过E作EF⊥OE交CB的延长线于F,则图中阴影部分的面积为2$\sqrt{2}$-2cm2.
如图:扇形DOE的圆心角为直角,它的半径为2cm,正方形OABC内接于扇形,点A、B、C分别在OE、$\widehat{DE}$、OD上,过E作EF⊥OE交CB的延长线于F,则图中阴影部分的面积为2$\sqrt{2}$-2cm2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在△ABC中,AD⊥BC,AE平分∠BAC.
如图,在△ABC中,AD⊥BC,AE平分∠BAC.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com