
【题目】如图表示的是汽车在行驶的过程中,速度随时间变化而变化的情况.
(1)汽车从出发到最后停止共经过了多少时间?它的最高时速是多少?
(2)汽车在那些时间段保持匀速行驶?时速分别是多少?
(3)出发后8分到10分之间可能发生了什么情况?
(4)用自己的语言大致描述这辆汽车的行驶情况.
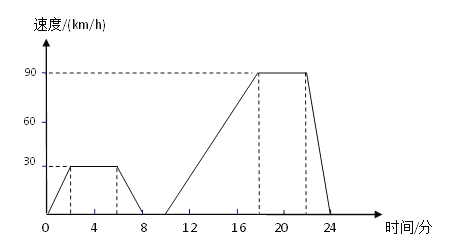
【答案】(1)汽车从出发到最后停止共经过了24min,它的最高时速是90km/h;(2)30km/h 和90km/h;(3)可能遇到了红灯或者障碍;(4)汽车出发2分钟后以30km/h的速度匀速行驶了4分钟,又减速行驶了2分钟,又停止了2分钟,后加速了8分钟到90km/h的速度匀速行驶了4分钟,最后2分钟停止了行驶。
【解析】(1)汽车从出发到最后停止共经过了24min,它的最高时速是90km/h
(2)汽车大约在2分到6分,18分到22分之间保持匀速行驶,时速分别是30km/h 和90km/h
(3)出发后8分到10分速度为0,所以汽车是处于静止的。可能遇到了红灯或者障碍(或者遇到了朋友或者休息)。(答案不唯一,只要所说的情况合理即可)
(4)该汽车出发2分钟后以30km/h的速度匀速行驶了4分钟,又减速行驶了2分钟,又停止了2分钟,后加速了8分钟到90km/h的速度匀速行驶了4分钟,最后2分钟停止了行驶。


科目:初中数学 来源: 题型:
【题目】一个不透明的口袋内装有50个大小材质相同且编号不同的小球,它们按照从1到50依次编号,将袋中的小球搅匀,然后从中随意取出一个小球,请问
(1)取出的小球编号是偶数的概率是多少?
(2)取出的小球编号是3的倍数的概率是多少?
(3)取出的小球编号是质数的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知正方形ABCD的边长为1,点P为正方形内一动点,若点M在AB上,且满足△PBC∽△PAM,延长BP交AD于点N,连结CM.
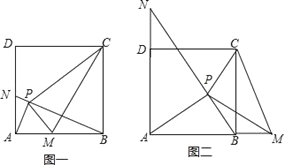
(1)如图一,若点M在线段AB上,求证:AP⊥BN;AM=AN;
(2)①如图二,在点P运动过程中,满足△PBC∽△PAM的点M在AB的延长线上时,AP⊥BN和AM=AN是否成立?
②是否存在满足条件的点P,使得PC=![]() ?(不需说明理由).
?(不需说明理由).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图在直角坐标系中,有菱形OABC,A点的坐标为(10,0),对角线OB、AC相交于D点,双曲线y= ![]() (x>0)经过D点,交BC的延长线于E点,且OBAC=160,则点E的坐标为( )
(x>0)经过D点,交BC的延长线于E点,且OBAC=160,则点E的坐标为( )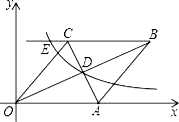
A.(5,8)
B.(5,10)
C.(4,8)
D.(3,10)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在比例尺为1:10000000的地图上,测得江华火车站到永州高铁站的距离是2cm ,那么江华火车站到永州高铁站的实际距离为( )km
A.20000000B.200000C.2000D.200
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,AB的垂直平分线交AB于点N,交BC的延长线于点M.

(1)若∠A=40°,求∠NMB的度数.
(2)如果将(1)中∠A的度数改为70°,其余条件不变,求∠NMB的度数.
(3)由(1)(2)你发现了什么规律?并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com