

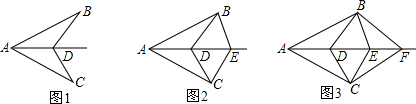
���� ��1����������ABD��������ACE��Ϊ����ֱ�������Σ����õ���ֱ�������ε����ʼ���ʽ�����ʵõ���DAC=��BAE������SAS�ɵó���DAC�ա�BAE����֤��
��2������C��CM��AB��M������G��GN��EA��EA�ӳ�����N���ó���ABC���AEG�������ߣ�����ֱ�������ε�������֤����ACM�ա�AGN�����жϡ�ABC���ADE���֮��Ĺ�ϵ�Ĺؼ���
��3��ͬ��2������֪��Ȧ�����������ε����֮�͵�����Ȧ�����������ε����֮�ͣ��������С·һ��ռ�ض���ƽ����
��� ��1��֤�����ߡ�ABD�͡�ACE��Ϊ����ֱ�������Σ�
��AD=AB��AE=AC����DAB=��EAC=90�㣬
���DAB+��BAC=��EAC+��BAC������DAC=��BAE��
�ڡ�DAC�͡�BAE�У�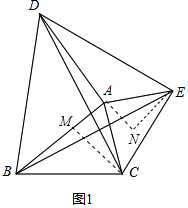 $\left\{\begin{array}{l}{AB=AD}\\{��DAC=��BAE}\\{AC=AE}\end{array}\right.$��
$\left\{\begin{array}{l}{AB=AD}\\{��DAC=��BAE}\\{AC=AE}\end{array}\right.$��
���DAC�ա�BAE��SAS����
��2����ABC���ADE�����ȣ�
֤�����ߡ�ABD�͡�ACE���ǵ���ֱ�������Σ�
���BAD=��CAE=90�㣬AB=AD��AC=AE��
�ߡ�BAD+��CAD+��BAC+��DAE=360�㣬
���BAC+��DAE=180�㣬
�ߡ�DAE+��EAN=180�㣬
���BAC=��EAN��
�ڡ�ACM�͡�AEN�У�$\left\{\begin{array}{l}{��MAC=��NAE}\\{��AMC=��ANE}\\{AC=AE}\end{array}\right.$
���ACM�ա�AEN��AAS����
��CM=EN��
��S��ABC=$\frac{1}{2}$AB•CM��S��ADE=$\frac{1}{2}$AD•EN��
��S��ABC=S��ADE��
��3���⣺�ɣ�2��֪��Ȧ�����������ε����֮�͵�����Ȧ�����������ε����֮�ͣ�
������С·�����Ϊ��30+2��20��=70ƽ���ף�
�ʴ�Ϊ��70��
���� �������ı����ۺ��⣬��Ҫ���������������ʣ�ȫ�������ε��ж������ʣ�����ؽ�������������ȫ�ȣ�Ѱ�����������֮��ĵ�����ϵ��������⣮�������ε�������֤����ACM�ա�ANE�����жϡ�ABC���ADE���֮��Ĺ�ϵ�Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
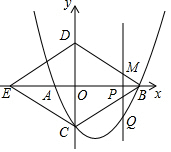 ��������x�ύ��A��B���㣬����B�ڵ�A����ࣩ��A��B���������ֱ�Ϊ��-2��0������8��0������y�ύ�ڵ�C��0��-4��������BC����BCΪһ�ߣ���OΪ�Գ�����������BDEC����P��x���ϵ�һ�����㣬���P������Ϊ��m��0��������P��x��Ĵ���L���������ڵ�Q����BD�ڵ�M��
��������x�ύ��A��B���㣬����B�ڵ�A����ࣩ��A��B���������ֱ�Ϊ��-2��0������8��0������y�ύ�ڵ�C��0��-4��������BC����BCΪһ�ߣ���OΪ�Գ�����������BDEC����P��x���ϵ�һ�����㣬���P������Ϊ��m��0��������P��x��Ĵ���L���������ڵ�Q����BD�ڵ�M���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
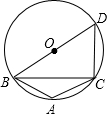 ��ͼ����ABC�ڽ��ڡ�O����BAC=120�㣬AB=AC��BDΪ��O��ֱ����AB=5����CD=5��
��ͼ����ABC�ڽ��ڡ�O����BAC=120�㣬AB=AC��BDΪ��O��ֱ����AB=5����CD=5���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
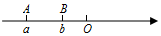 ��֪a��b��ʾ������ͬ��A��B������������|a|=5��|b|=2�������������λ����ͼ��ʾ��
��֪a��b��ʾ������ͬ��A��B������������|a|=5��|b|=2�������������λ����ͼ��ʾ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com