
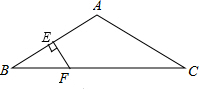
 如图,△ABC中,AB=AC,∠A=120°,AB的垂直平分线EF交AB于E,交BC于F.求证:CF=2BF.
如图,△ABC中,AB=AC,∠A=120°,AB的垂直平分线EF交AB于E,交BC于F.求证:CF=2BF. 分析 连接AF,根据等腰三角形两底角相等求出∠B=∠C=30°,根据线段垂直平分线上的点到线段两端点的距离相等可得AF=BF,根据等边对等角求出∠BAF,再求出∠CAF=90°,然后根据直角三角形30°角所对的直角边等于斜边的一半证明即可.
解答 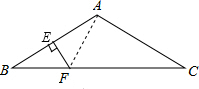 证明:如图,连接AF,
证明:如图,连接AF,
∵AB=AC,∠A=120°,
∴∠B=∠C=$\frac{1}{2}$×(180°-120°)=30°,
∵EF垂直平分AB,
∴AF=BF,
∴∠BAF=∠B=30°,
∴∠CAF=∠BAC-∠BAF=120°-30°=90°,
∴CF=2AF,
∴CF=2BF.
点评 本题考查了等腰三角形的性质,线段垂直平分线上的点到线段两端点的距离相等的性质,直角三角形30°角所对的直角边等于斜边的一半,熟记各性质是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在直角坐标系中,已知点A的坐标为(6,0),点B(x,y)在第一象限内,且满足x+y=8,设△AOB的面积是S.
如图,在直角坐标系中,已知点A的坐标为(6,0),点B(x,y)在第一象限内,且满足x+y=8,设△AOB的面积是S.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com