
分析 (1)由根的判别式和根与系数的关系即可得出结果;
(2)由互为相反数的关系和根与系数的关系得出m=1,代入判别式得出△<0,即可得出结果;
(3)由根的判别式和根与系数的关系即可得出结果.
解答 解:(1)∵方程x2-4x+3m+1=0有两个不相等的正数根,
∴△=16-4(3m+1)>0,且3m+1>0,
解得:m<1,且m>-$\frac{1}{3}$,
∴-$\frac{1}{3}$<m<1;
(2)∵方程x2-(m-1)x+3=0的两根是互为相反数,
∴m-1=0,
解得:m=1,
此时,△=[-(m-1)]2-4×1×3<0,方程无解,
∴方程x2-(m-1)x+3=0的两根不能是互为相反数;
(3)∵方程2x2+x-2m+1=0的两根异号,
∴-2m+1<0,且△=12-4×2×(-2m+1)>0,
∴m>$\frac{1}{2}$,且m>$\frac{7}{16}$,
∴m>$\frac{1}{2}$时,方程2x2+x-2m+1=0的两根异号.
点评 本题考查了根的判别式、根与系数的关系;熟练掌握根与系数的关系是解决问题的关键.


 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案科目:初中数学 来源: 题型:选择题
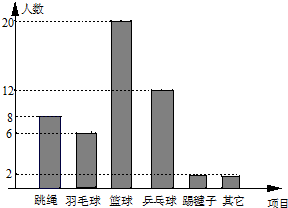 小程对本班50名同学进行了“我最喜爱的运动项目”的调查,统计出了最喜爱跳绳、羽毛球、篮球、乒乓球、踢毽子等运动项目的人数,并根据调查结果绘制了如图所示的条形统计图.若将条形统计图转化为扇形统计图,那么最喜爱打篮球的人数所在扇形区域的圆心角的度数为( )
小程对本班50名同学进行了“我最喜爱的运动项目”的调查,统计出了最喜爱跳绳、羽毛球、篮球、乒乓球、踢毽子等运动项目的人数,并根据调查结果绘制了如图所示的条形统计图.若将条形统计图转化为扇形统计图,那么最喜爱打篮球的人数所在扇形区域的圆心角的度数为( )| A. | 144° | B. | 75° | C. | 180° | D. | 150° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com