
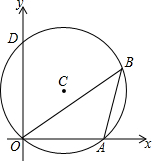
 如图,⊙C经过原点,并与两坐标轴分别交于A、D两点,已知∠OBA=60°,点D的坐标为(0,2),求点A与圆心C的坐标.
如图,⊙C经过原点,并与两坐标轴分别交于A、D两点,已知∠OBA=60°,点D的坐标为(0,2),求点A与圆心C的坐标. 分析 首先连接AD,过点C作CE⊥x轴于点E,由90°的圆周角所对的弦是直径,可得AD是直径,然后由圆周角定理,可得∠ODA=60°,继而求得AD与OA的长,则可求得点A的坐标,然后由垂径定理求得CE与OE的长,即可求得点C的坐标.
解答  解:连接AD,过点C作CE⊥x轴于点E,
解:连接AD,过点C作CE⊥x轴于点E,
∵∠AOD=90°,
∴AD是直径,
∵∠ODA=∠OBA=60°,
∴∠OAD=30°,
∵点D的坐标为(0,2),
∴OD=2,
∴AD=2OD=4,
∴OA=$\sqrt{A{D}^{2}-O{D}^{2}}$=2$\sqrt{3}$,
∴点A的坐标为:(2$\sqrt{3}$,0);
∴OE=$\frac{1}{2}$OA=$\sqrt{3}$,CE=$\frac{1}{2}$OD=1,
∴点C的坐标为:($\sqrt{3}$,1).
点评 此题考查了圆周角定理以及垂径定理.注意掌握辅助线的作法.


科目:初中数学 来源: 题型:解答题
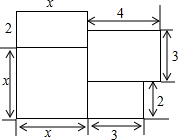 如图,是一所住宅的平面图(图中长度单位:m).
如图,是一所住宅的平面图(图中长度单位:m).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com