
【题目】如图,等腰直角△ABC中,∠ABC=90°,点D在AC上,将△ABD绕顶点B沿顺时针方向旋转90°后得到△CBE.
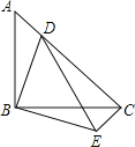
(1)求∠DCE的度数;
(2)当AB=8,AD∶DC=1∶3时,求DE的长.
【答案】(1)求∠DCE的度数为90°;
(2)DE的长为![]()
【解析】试题分析:(1)利用等腰直角三角形的性质以及旋转的性质得出∠DCE=∠ACB+∠BCE,即可得出答案;
(2)利用勾股定理得出AC的长,再利用旋转的性质得出AD=CE,进而利用勾股定理得出DE的长.
试题解析:(1)∵△CBE是由△ABD旋转得到的,
∴△ABD≌△CBE,∴∠A=∠BCE=45°,
∴∠DCE=∠DCB+∠BCE=90°.
(2)在等腰直角三角形ABC中,∵AB=8,∴AC=![]() ,
,
又∵AD:DC=1:3,∴AD =![]() ,DC=
,DC=![]() .
.
由(1)知AD=CE且∠DCE=90°,∴DE2=DC2+CE2=72+8=80,
∴DE=![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】用两个全等的直角三角形拼下列图形:(1)平行四边形(不包含菱形、矩形、正方形);(2)矩形;(3)正方形;(4)等腰三角形,一定可以拼成的图形是 ( )
A、(1)(2)(4) B、(2)(3)(4) C、(1)(3)(4) D、(1)(2)(3)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,AB=AC,BD、CE是高,BD与CE相交于点O.
(1)求证:OB=OC;
(2)若∠ABC=55°,求∠BOC的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近似数38.57的取值范围是( )
A. 38.565 ≤ a<38.575 B. 38.565<a <38.575
C. 38.565<a ≤38.575 D. 38.55 ≤ a<38.65
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】你知道为什么任何无限循环小数都可以写成分数形式吗?下面的解答过程会告诉 你原因和方法.
(1)阅读下列材料:
问题:利用一元一次方程将![]() 化成分数.
化成分数.
设 ![]() .
.
由![]() ,可知
,可知 ![]() ,
,
即 ![]() .(请你体会将方程两边都乘以10起到的作用)
.(请你体会将方程两边都乘以10起到的作用)
可解得 ![]() ,即
,即 ![]() .填空:将
.填空:将![]() 写成分数形式为 .
写成分数形式为 .
(2)请仿照上述方法把小数![]() 化成分数,要求写出利用一元一次方程进行解答的过程.
化成分数,要求写出利用一元一次方程进行解答的过程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com