
����Ŀ����ͼ���������������Ϊ1�ĵ���ֽ�ϣ��������ڻ��������ڵ�����֮��ľ��붼��1����λ���ȣ����������㶼�ڵ����ϵ������ν������������Σ��밴Ҫ��������в�����

��1����������ABCˮƽ����ƽ��4����λ���ȣ�����ֱ����ƽ��5����λ���ȣ�����ƽ�ƺ����A1B1C1��
��2������AA1��BB1�����߶�AA1��BB1��λ�ù�ϵΪ�� ��������ϵΪ�� �������߶�AA1�ij��ȴ�Լ���� ��AA1���� ��λ���ȣ�����д����������������
��3��������ABC��AB�ϵĸ�CD��
���𰸡���1������������2���߶�AA1�ij��ȴ�Լ��6��AA1��7��λ���ȣ���3����������
��������
��1�����ݡ�ABCˮƽ����ƽ��4����λ���ȣ�����ֱ����ƽ��5����λ���ȣ����ɻ���ƽ�ƺ�ġ�A1B1C1��
��2������ƽ�Ƶ����ʣ����ɵõ��߶�AA1��BB1��λ�ù�ϵ�Լ�������ϵ�����ݹ��ɶ������ɹ����߶�AA1�ij��ȣ�
��3�����ݵ����ABC�������λ�ã���������л����ߵķ��������ɵó���ABC��AB�ϵĸ�CD��
��1����ͼ��ʾ����A1B1C1��Ϊ����

��2����ƽ�Ƶ�����֪���߶�AA1��BB1��λ�ù�ϵΪƽ�У�������ϵΪ��ȣ�
�ɹ��ɶ����ɵã�AA1�ij���Ϊ![]() ��
��
���߶�AA1�ij��ȴ�Լ��6��AA1��7��λ���ȣ�
��3����ͼ��ʾ��CD��Ϊ����


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڳ�����ABCD�У�AB��8cm��BC��6cm����E��CD���ϵ�һ�㣬��DE��2cm������P��A���������2cm/s���ٶ���A��B��C��E�˶������յ����E.����APE���������20cm2ʱ�����P�˶���ʱ��Ϊ___________.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ں��������Ϻ��ʵ����ݣ���������֤����
��ͼ������AH������ACGFEN�ڵ�B��D��E����֪��A=��1����C=��F��BMƽ�֡�CBD��ENƽ�֡�FEH����֤����2=��3��

֤�����ߡ�A=��1����֪��
��AC��GF�� ��
�ࣨ ���� ��
�ߡ�C=��F����֪��
���F=��G
�ࣨ ���� ��
�ࣨ ���� ��
��BMƽ�֡�CBD��ENƽ�֡�FEH
���2= ��3=
���2=��3
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У�CD��AB������ΪD����E��BC�ϣ�EF��AB������ΪF.

(1) CD��EFƽ����Ϊʲô��
(2)�����1=��2���ҡ�3=115�������ACB�Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵxOy�У�������![]() ������A��-3��4����
������A��-3��4����
��1����b��ֵ��
��2������A��![]() ���ƽ���߽�����������һ��B����ֱ��AB����ȡһ��P������A����ֱ��OP�ĶԳƵ�C��
���ƽ���߽�����������һ��B����ֱ��AB����ȡһ��P������A����ֱ��OP�ĶԳƵ�C��
�ٵ���Cǡ������![]() ��ʱ����ֱ��OP�ı���ʽ��
��ʱ����ֱ��OP�ı���ʽ��
������BC����BC����Сֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪������ABCD�ĶԽ��߳�Ϊ2![]() ����������ABCD��ֱ��EF�۵�����ͼ����Ӱ���ֵ��ܳ�Ϊ��������
����������ABCD��ֱ��EF�۵�����ͼ����Ӱ���ֵ��ܳ�Ϊ��������

A. 8![]() B. 4
B. 4![]() C. 8 D. 6
C. 8 D. 6
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
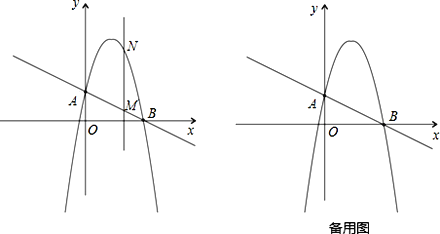
����Ŀ����ͼ��һ�κ���![]() �ֱ�y�ᡢx ����A��B���㣬������
�ֱ�y�ᡢx ����A��B���㣬������![]() ��A��B����.
��A��B����.
��1������������ߵĽ���ʽ��
��2������ֱx���ֱ��x=t���ڵ�һ����ֱ��AB�ڵ�M��������������ڵ�N.��t ȡ��ֵʱ��MN�����ֵ�����ֵ�Ƕ��٣�
��3������2��������£���A��M��N��DΪ������ƽ���ı��Σ�����ĸ�����D������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı���ABCD�ڽ��ڡ�O��AD��BC���ӳ����ཻ�ڵ�E��AB��DC���ӳ����ཻ�ڵ�F������E����F��80�������A��____�㣮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��A��a��2b��2��4ab����������y=x2+4x+10�ϣ����A���������߶Գ���ĶԳƵ�����Ϊ��������
A. ����3��7�� B. ����1��7�� C. ����4��10�� D. ��0��10��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com