
【题目】在△ABC中,过A作BC的平行线,交∠ACB的平分线于点D,点E是BC上一点,连接DE,交AB于点F,∠DEB+∠CAD=180°.
(1)如图1,求证:四边形ACED是菱形;
(2)如图2,G是AD的中点,H是AC边中点,连接CG、EG、EH,若∠ACB=90°,BC=2AC,在不添加任何辅助线的情况下,请直接写出图中与△CEH全等的三角形(不含△CEH本身).
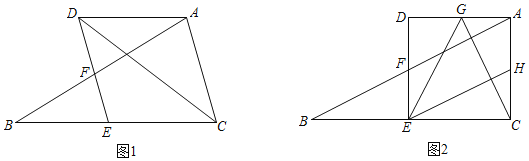
【答案】(1)见解析;(2)△BEF,△ADF,△EDG,△CAG
【解析】
(1)先证明四边形ACED是平行四边形,然后通过证明AD=AC,于是可得到结论;
(2)根据已知条件得到菱形ACED是正方形,求得∠D=∠CAG=∠DEC=90°,AC=AD=CE,根据全等三角形的判定定理即可得到结论.
(1)证明:∵AD//BC,
∴∠ADE=∠DEB,
∵∠DEB+∠DEC=180°,∠DEB+∠CAD=180°,
∴∠DEC=∠DAC,
∴∠ADE+∠DAC=180°,
∴DE//AC,
∴四边形ACED是平行四边形,
∵AD//BC,
∴∠ADC=∠BCD,
∵CD平分∠ACB,
∴∠ACD=∠BCD,
∴∠ADC=∠ACD,
∴AD=AC,
∴四边形ACED是菱形;
(2)解:∵四边形ACED是菱形,∠ACB=90°,
∴菱形ACED是正方形,
∴∠D=∠CAG=∠DEC=90°,
AC=AD=CE,
∵G是AD的中点,H是AC边中点,
∴AG=DG=![]() CE,
CE,
∴△EDG≌△CAG≌△ECH(SAS),
∵BC=2AC,
∴BE=CE=AD,
∵AD//BE,
∴∠B=∠DAF,
∵∠AFD=∠BFE,
∴△BFE≌△ADF(AAS),
∴EF=DF=![]() ,
,
∴EF=CH,
∴△BEF≌△ECH(SAS),
∴图中与△CEH全等的三角形有△BEF,△ADF,△EDG,△CAG.


科目:初中数学 来源: 题型:
【题目】如图,已知△ABC,∠B=90゜,AB=3,BC=6,动点P、Q同时从点B出发,动点P沿BA以1个单位长度/秒的速度向点A移动,动点Q沿BC以2个单位长度/秒的速度向点C移动,运动时间为t秒.连接PQ,将△QBP绕点Q顺时针旋转90°得到△![]() ,设△
,设△![]() 与△ABC重合部分面积是S.
与△ABC重合部分面积是S.
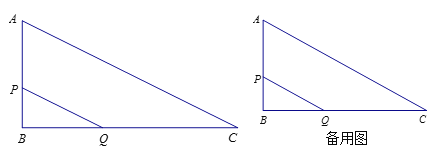
(1)求证:PQ∥AC;
(2)求S与t的函数关系式,并直接写出自变量t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,关于x的方程x2+2x-k=0有两个不相等的实数根.
(1)求k的取值范围;
(2)若x1,x2是这个方程的两个实数根,求![]() 的值;
的值;
(3)根据(2)的结果你能得出什么结论?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=-2,与x轴的一个交点在(-3,0)和(-4,0)之间,其部分图象如图所示.则下列结论:①4a-b=0;②c<0;③-3a+c>0;④4a-2b>at2+bt(t为实数);⑤点![]() ,
,![]() ,
,![]() 是该抛物线上的点,则y1<y2<y3.其中正确结论的个数是( )
是该抛物线上的点,则y1<y2<y3.其中正确结论的个数是( )
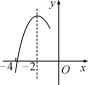
A.4B.3C.2D.1
查看答案和解析>>
科目:初中数学 来源: 题型:
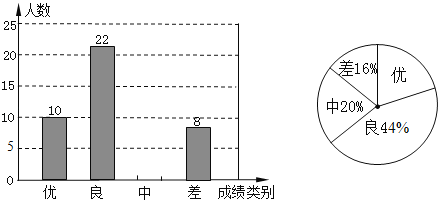
【题目】为迎接2016年中考,某中学对全校九年级学生进行了一次数学模拟考试,并随机抽取了部分学生的测试成绩作为样本进行分析,绘制成如下两幅不完整的统计图,请你根据统计图中提供的信息解答下列问题:
(1)这次调査中,一共抽取了多少名学生?
(2)求样本中表示成绩为“中”的人数,并将条形统计图补充完整;
(3)该学校九年级共有1000人参加了这次数学考试,估计该校九年级共有多少名学生的数学成绩可以达到优秀?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,荧光屏上的甲、乙两个光斑(可看作点)分别从相距8cm的A,B两点同时开始沿线段AB运动,运动工程中甲光斑与点A的距离S1(cm)与时间t(s)的函数关系图象如图2,乙光斑与点B的距离S2(cm)与时间t(s)的函数关系图象如图3,已知甲光斑全程的平均速度为1.5cm/s,且两图象中△P1O1Q1≌P2Q2O2,下列叙述正确的是( )

A. 甲光斑从点A到点B的运动速度是从点B到点A的运动速度的4倍
B. 乙光斑从点A到B的运动速度小于1.5cm/s
C. 甲乙两光斑全程的平均速度一样
D. 甲乙两光斑在运动过程中共相遇3次
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,P是矩形ABCD内部的一定点,M是AB边上一动点,连接MP并延长与矩形ABCD的一边交于点N,连接AN.已知AB=6cm,设A,M两点间的距离为xcm,M,N两点间的距离为y1cm,A,N两点间的距离为y2cm.小欣根据学习函数的经验,分别对函数y1,y2随自变量x的变化而变化的规律进行了探究.下面是小欣的探究过程,请补充完整;
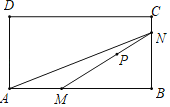
(1)按照如表中自变量x的值进行取点、画图、测量,分别得到了y1,y2与x的几组对应值;
x/cm | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
y1/cm | 6.30 | 5.40 |
| 4.22 | 3.13 | 3.25 | 4.52 |
y2/cm | 6.30 | 6.34 | 6.43 | 6.69 | 5.75 | 4.81 | 3.98 |
(2)在同一平面直角坐标系xOy中,描出以补全后的表中各组对应值所对应的点(x,y1),并画出函数y1的图象;
(3)结合函数图象,解决问题:当△AMN为等腰三角形时,AM的长度约为 cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
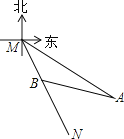
【题目】如图,射线MN表示一艘轮船的航行路线,从M到N的走向为南偏东30°,在M的南偏东60°方向上有一点A,A处到M处为100海里.
(1)求点A到航线MN的距离;
(2)在航线MN上有一点B,且∠MAB=15°,若轮船的速度为50海里/时,求轮船从M处到B处所用时间为多少小时?(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线l和双曲线y=![]() (k>0)交于A、B两点,P是线段AB上的点(不与A、B重合),过点A、B、P分别向x轴作垂线,垂足分别为C、D、E,连接OA、OB、OP,设△AOC的面积为S1、△BOD的面积为S2、△POE的面积为S3,则( )
(k>0)交于A、B两点,P是线段AB上的点(不与A、B重合),过点A、B、P分别向x轴作垂线,垂足分别为C、D、E,连接OA、OB、OP,设△AOC的面积为S1、△BOD的面积为S2、△POE的面积为S3,则( )
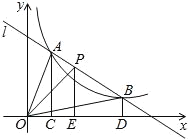
A.S1<S2<S3B.S1>S2>S3C.S1=S2>S3D.S1=S2<S3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com