Question

1．已知：如图l，在平面直角坐标系中，0是坐标原点，Rt△AOB和Rt△CDE各有一边0B、CE在x轴上．∠ABO=∠BDE=90°，CE=4，A、D、E三点在一条直线上，该直线的解析式为y=-x+7，与x轴、y轴分别交于E、F两点．
（1）点E的坐标为（7，0），点A的坐标为（3，4），过原点和点A、E的抛物线解析式为y=-$\frac{1}{3}$x²+$\frac{7}{3}$x．
（2）Rt△CDE从图1的位置出发，以1每秒一个单位的速度沿B0向点0匀速运动，当点E运动到与点B重合时停止运动．设Rt△AOB与Rt△CDE重合部分的面积为S，运动时间为t秒，请求出S与t之间的函数关系式．
（3）如图2，若点M在直线AB上，∠BMO+∠BAO=∠AEO，求AM的长．

Answer 1

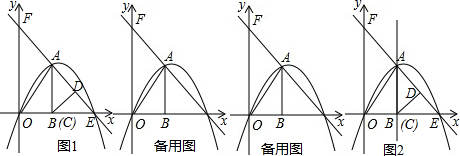
分析 （1）只需令y=0就可求出点E的坐标，从而得到OE、OB，就可得到点A的坐标，然后运用待定系数法就可求出抛物线的解析式；
（2）由于△CDE向左平移的过程中，△AOB与△CDE重合部分的形状发生变化，需分情况讨论，若重合部分直接求比较困难，运用割补法就可解决问题；
（3）由于点M在直线AB上，可分点M在点B的下方和点M在点B的上方进行讨论，①当点M在点B的下方时，过点A作AN⊥OM于N，如图2，根据三角形外角的性质可得∠AON=45°，运用三角函数可求出AN，易证△OBM∽△ANM，根据相似三角形的性质可得OM=$\frac{3\sqrt{2}}{5}$AM．设BM=x，则有OM=$\frac{3\sqrt{2}}{5}$（x+4），在Rt△OBM中运用勾股定理就可求出x，即可得到AM的值；②若点M在点B的上方，此时点M与点B下方的点M关于x轴对称，因而BM的值相同，从而可求出AM的值．

解答 解：（1）∵直线y=-x+7与x轴交于E点．
∴将y=0代入y=-x+7得，x=7．
∴点E的坐标为（7，0），OE=7．
∵CE=4，
∴OC=3．
将x=3代入y=-x+7，得y=4，
∴点A的坐标为（3，4）．
设过原点和点A、E的抛物线解析式为y=ax²+bx+c，
则有$\left\{\begin{array}{l}{c=0}\\{9a+3b+c=4}\\{49a+7b+c=0}\end{array}\right.$
解得：$a=-\frac{1}{3}，b=\frac{7}{3}$，c=0
∴过原点和点A、E的抛物线解析式为y=-$\frac{1}{3}$x²+$\frac{7}{3}$x．
故答案分别为：（7，0），（3，4），y=-$\frac{1}{3}$x²+$\frac{7}{3}$x；

（2）如图1，∵AB=BE=4，∠ABE=90°，
∴∠AEB=∠BAE=45°，即∠DEB=45°．
∵∠CDE=90°，CE=4，
∴DE=DC=CE•sin∠DEC=4×$\frac{\sqrt{2}}{2}$=2$\sqrt{2}$，
∴S_△CDE=$\frac{1}{2}$×2$\sqrt{2}$×$2\sqrt{2}$=4．
由题可得OE=7-t，BC=t．
①当0≤t≤2时，如图a，

S=S_△CBP=$\frac{1}{2}$CB•BP=$\frac{1}{2}$t²；
②当2＜t≤3时，如图b，

S=S_△CDE-S_△PBE
=4-$\frac{1}{2}$（4-t）²
=-$\frac{1}{2}$t²+4t-4；
③当3＜t≤$\frac{7}{2}$时，如图c，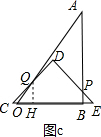

设CD与AO交于点Q，过点Q做QH⊥BC于H，
则有tan∠AOB=$\frac{QH}{OH}$=$\frac{AB}{OB}$=$\frac{4}{3}$，
∴OH=$\frac{3}{4}$QH．
∵tan∠QCH=$\frac{QH}{CH}$=tan45°=1，
∴QH=CH，
∴CO=CH-OH=QH-$\frac{3}{4}$QH=$\frac{1}{4}$QH，
∴QH=4CO=4（t-3），
∴S_△COQ=$\frac{1}{2}$CO•QH=$\frac{1}{2}$（t-3）•4（t-3）=2t²-12t+18，
S_△PBE=$\frac{1}{2}$（4-t）²=8-4t+$\frac{1}{2}$t²，
∴S=S_△CDE-S_△COQ-S_△PBE=-$\frac{5}{2}$t²+16t-22；
④当$\frac{7}{2}$＜t≤4时，如图d，

设DE与OA交于点S，过点S作ST⊥BC于T，
∵tan∠AOB=$\frac{ST}{OT}$=$\frac{AB}{OB}$=$\frac{4}{3}$，tan∠DEC=$\frac{ST}{TE}$=tan45°=1，
∴OT=$\frac{3}{4}$ST，TE=ST，
∴OE=OT+TE=$\frac{7}{4}$ST=7-t，
∴ST=4-$\frac{4}{7}$t，
∴S_△SOE=$\frac{1}{2}$OE•ST=$\frac{1}{2}$（7-t）（4-$\frac{4}{7}$t）=14-4t+$\frac{2}{7}$t²，
∴S=S_△SOE-S_△PBE=（14-4t+$\frac{2}{7}$t²）-（8-4t+$\frac{1}{2}$t²）=-$\frac{3}{14}$t²+6．
综上所述：S=$\left\{\begin{array}{l}{\frac{1}{2}{t}^{2}，0≤t≤2}\\{-\frac{1}{2}{t}^{2}+4t-4，2＜t≤3}\\{-\frac{5}{2}{t}^{2}+16t-22，3＜t≤\frac{7}{2}}\\{-\frac{3}{14}{t}^{2}+6，\frac{7}{2}＜t≤4}\end{array}\right.$

（3）①若点M在点B的下方，过点A作AN⊥OM于N，如图2，

则有∠AON=∠BMO+∠BAO=∠AEO=45°，
∴AN=AO•sin45°=$\frac{\sqrt{2}}{2}$•$\sqrt{{3}^{2}+{4}^{2}}$=$\frac{5\sqrt{2}}{2}$．
∵∠OMB=∠AMN，∠OBM=∠ANM=90°，
∴△OBM∽△ANM，
∴$\frac{OM}{AM}$=$\frac{OB}{AN}$=$\frac{3}{\frac{5\sqrt{2}}{2}}$=$\frac{3\sqrt{2}}{5}$，
∴OM=$\frac{3\sqrt{2}}{5}$AM．
设BM=x，则有AM=x+4，OM=$\frac{3\sqrt{2}}{5}$（x+4）．
在Rt△OBM中，
[$\frac{3\sqrt{2}}{5}$（x+4）]²=3²+x²，
整理得：7x²-144x-63=0，
解得：x₁=-$\frac{3}{7}$（舍去），x₂=21，
∴AM=AB+BM=4+21=25．
②若点M在点B的上方，
则有BM=21，AM=BM-AB=21-4=17．
综上所述：AM的长为25或17．

点评 本题主要考查了直线与x轴的交点、用待定系数法求抛物线的解析式、运用三角函数解三角形、相似三角形的判定与性质、勾股定理、解一元二次方程等知识，对运算能力要求比较高，运用分类讨论和割补法是解决第（2）小题的关键，运用外角的性质得到∠AON=45°，然后将三角形相似与勾股定理相结合是解决第（3）小题的关键．在解决问题的过程中，借助于勾股定理、三角函数、相似三角形性质建立方程，是初中阶段常用的方法，应熟练掌握．