
| 1 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 1 |
| A | 2 | 2 |
| 2 | 2 | 2 |
| 2 | 2 | 2 |
分析 对照两表,可知:要将1变成2必须经过奇数次操作,要将0变成2必须经过偶数次操作,而所有的1都与偶数个格子相邻,所有的0都与奇数个格子相邻.最简的方法就是让0通过2次加上1的操作变成2,即0+1+1,让1通过1次加上1的操作变成2,即1+1.如下图:按题中要求操作,图中阴影方格的数字之和与空白方格的数字之和的差不变.因此A的数值为A=(1+1+1+1+1)-(0+0+0+0)=5.解决问题.
解答  解:图中阴影方格的数字之和与空白方格的数字之和的差不变.
解:图中阴影方格的数字之和与空白方格的数字之和的差不变.
A=(1+1+1+1+1)-(0+0+0+0)=5.
故答案为:5.
点评 根据图示,抓住“阴影方格的数字之和与空白方格的数字之和的差不变”进行解答.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 6$\sqrt{3}$ | B. | 6 | C. | 3$\sqrt{3}$ | D. | 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图所示,在△ABC中,AB=AC,P是BC边上的一点,PE⊥AC,PF⊥AB,BD是AC边上的高,若PE=5cm,PF=3cm,求CD的长.
如图所示,在△ABC中,AB=AC,P是BC边上的一点,PE⊥AC,PF⊥AB,BD是AC边上的高,若PE=5cm,PF=3cm,求CD的长.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 以满足|x|+|y|=1的所有的对数(x,y)为坐标原点,构成了一个正方形MNPQ(如图所示),这个正方形被直线l:y=ax-a-1分成了两部分.
以满足|x|+|y|=1的所有的对数(x,y)为坐标原点,构成了一个正方形MNPQ(如图所示),这个正方形被直线l:y=ax-a-1分成了两部分.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
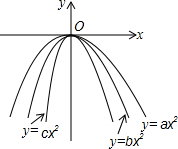 在同一平面直角坐标系内,二次函数y=ax2、y=bx2、y=cx2的图象如图所示,则a、b、c的大小关系是( )
在同一平面直角坐标系内,二次函数y=ax2、y=bx2、y=cx2的图象如图所示,则a、b、c的大小关系是( )| A. | a>b>c | B. | c>b>a | C. | b>c>a | D. | c>a>b |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com