

·ÖÎö Łš1Ł©žùŸĘMQŽčÖ±ÓÚMPŁŹMNŽčÖ±ÓÚBCŁŹÀûÓĂ”ÈÊœ”ÄĐÔÖÊ”Ă”œÒ»¶ÔœÇÏà”ÈŁŹÔÙÀûÓĂÍŹœÇ”ÄÓàœÇÏà”È”Ă”œÒ»¶ÔœÇÏà”ÈŁŹÀûÓĂÁœœÇÏà”È”ÄÈęœÇĐÎÏàËÆŒŽżÉ”ĂÖ€Ł»
Łš2Ł©PQ2=BP2+CQ2ŁŹÀíÓÉÈçÏÂŁșÈçÍŒ1ŁŹŃÓł€QMÖÁDŁŹÊčMD=MQŁŹÁŹœáBDĄąPDŁŹÀûÓĂSAS”Ă”œÈęœÇĐÎBDMÓëÈęœÇĐÎCQMÈ«”ÈŁŹÀûÓĂÈ«”ÈÈęœÇĐΔĶÔÓŠœÇÏà”ÈŁŹ¶ÔÓŠ±ßÏà”È”Ă”œÒ»¶ÔÄÚŽíœÇÏà”ÈŁŹœű¶űÈ·¶šłöBDÓëCQÆœĐĐÇÒÏà”ÈŁŹÀûÓĂÁœÖ±ÏßÆœĐĐÍŹĆÔÄڜǻ„Č裏”Ă”œĄÏPBDÎȘÖ±œÇŁŹÀûÓĂčŽčɶšÀíÁĐłöčŰϔʜŁŹ”ÈÁżŽú»»ŒŽżÉ”ĂÖ€Ł»
Łš3Ł©ÓÉMÎȘBCÖД㣏ÇółöCM”Äł€ŁŹÔÚÖ±œÇÈęœÇĐÎMNCÖĐŁŹÀûÓĂÈńœÇÈęœÇșŻÊ궚ÒćÇółöMN”Äł€ŁŹąÙÉèQ”ă”ÄÔ˶ŻËÙ¶ÈÎȘvcm/sŁŹÈçÍŒ1ŁŹ”±0ĄÜtŁŒ2$\sqrt{3}$ʱŁŹÓÉŁš1Ł©ÖȘĄśPBMĄŚĄśQNMŁŹÓÉÏàËÆ”Ă±ÈÀęÇółöQËÙ¶ÈŁŹÈçÍŒ2ŁŹÒŚÖȘ”±tĄĘ2$\sqrt{3}$ʱŁŹQ”ÄËÙ¶ÈŁ»ąÚÓÉAC-NC±íÊŸłöANŁŹÈçÍŒ1ŁŹ”±0ĄÜtŁŒ2$\sqrt{3}$ʱŁŹžùŸĘAPŁŹAQŁŹ±íÊŸłöSŁ»ÈçÍŒ2ŁŹ”±tĄĘ2$\sqrt{3}$ʱŁŹÍŹÀí±íÊŸłöAPŁŹAQŁŹœű¶ű±íÊŸłöSŒŽżÉŁź
œâŽđ Łš1Ł©Ö€ĂśŁșÈçÍŒ1ŁŹĄßMQĄÍMPŁŹMNĄÍBCŁŹ
ĄàĄÏPMB+ĄÏPMN=90ĄăŁŹĄÏQMN+ĄÏPMN=90ĄăŁŹ
ĄàĄÏPMB=QMNŁŹ
ĄßĄÏPBM+ĄÏC=90ĄăŁŹĄÏQNM+ĄÏC=90ĄăŁŹ
ĄàĄÏPBM=ĄÏQNMŁŹ
ĄàĄśPBMĄŚĄśQNMŁ»
Łš2Ł©œâŁșPQ2=BP2+CQ2ŁŹÀíÓÉÈçÏÂŁșÈçÍŒ1ŁŹŃÓł€QMÖÁDŁŹÊčMD=MQŁŹÁŹœáBDĄąPDŁŹ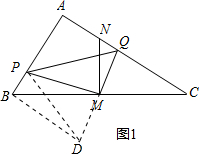
ĄßBCĄąDQ»„ÏàÆœ·ÖŁŹ
ĄàBM=CMŁŹDM=QMŁŹ
ÔÚĄśBDMșÍĄśCQMÖĐŁŹ
$\left\{\begin{array}{l}{BM=CM}\\{ĄÏBMD=ĄÏCMQ}\\{DM=QM}\end{array}\right.$ŁŹ
ĄàĄśBDMĄŐĄśCQMŁšSASŁ©ŁŹ
ĄàĄÏCQM=ĄÏBDMŁŹBD=CQŁŹ
ĄàBDĄÎCQŁŹ
ĄßĄÏBAC=90ĄăŁŹ
ĄàĄÏPBD=90ĄăŁŹ
ĄàPD2=BP2+BD2=BP2+CQ2ŁŹ
ĄßPMŽčֱƜ·ÖDQŁŹ
ĄàPQ=PDŁŹ
ÔòPQ2=BP2+CQ2Ł»
Łš3Ł©œâŁșĄßBC=8cmŁŹMÎȘBC”ÄÖД㣏
ĄàBM=CM=4cmŁŹ
ĄßĄÏABC=60ĄăŁŹĄÏC=30ĄăŁŹ
ĄàMN=$\frac{\sqrt{3}}{3}$CM=$\frac{{4\sqrt{3}}}{3}$cmŁ»
ąÙÉèQ”ă”ÄÔ˶ŻËÙ¶ÈÎȘvcm/sŁŹ
ÈçÍŒ1ŁŹ”±0ĄÜtŁŒ2$\sqrt{3}$cmʱŁŹÓÉŁš1Ł©ÖȘĄśPBMĄŚĄśQNMŁŹ
Ąà$\frac{NQ}{BP}$=$\frac{MN}{MB}$ŁŹŒŽ$\frac{vt}{2t}$=$\frac{\frac{4\sqrt{3}}{3}}{4}$ŁŹ
Ąàv=$\frac{2\sqrt{3}}{3}$cm/sŁ»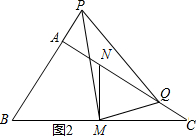
ÈçÍŒ2ŁŹÒŚÖȘ”±tĄĘ2$\sqrt{3}$ʱŁŹv=$\frac{2\sqrt{3}}{3}$cm/sŁŹ
ŚÛÉÏËùÊöŁŹQ”ăÔ˶ŻËÙ¶ÈÎȘ$\frac{2\sqrt{3}}{3}$cm/sŁ»
ąÚĄßBC=8cmŁŹAB=4cmŁŹAC=4$\sqrt{3}$cmŁŹNC=$\frac{8\sqrt{3}}{3}$cmŁŹ
ĄàAN=AC-NC=4$\sqrt{3}$-$\frac{8\sqrt{3}}{3}$=$\frac{4\sqrt{3}}{3}$cmŁŹ
ĄàÈçÍŒ1ŁŹ”±0ĄÜtŁŒ2$\sqrt{3}$cmʱŁŹAP=Łš4-2tŁ©cmŁŹAQ=AN+NQ=Łš$\frac{4\sqrt{3}}{3}$+$\frac{2\sqrt{3}}{3}$tŁ©cmŁŹ
ĄàS=$\frac{1}{2}$AP•AQ=$\frac{1}{2}$Łš4-2tŁ©Łš$\frac{4\sqrt{3}}{3}$+$\frac{2\sqrt{3}}{3}$tŁ©=Łš-$\frac{2\sqrt{3}}{3}$t2+$\frac{8\sqrt{3}}{3}$Ł©cm2Ł»
ÈçÍŒ2ŁŹ”±tĄĘ2$\sqrt{3}$cmʱŁŹAP=Łš2t-4Ł©cmŁŹAQ=AN+NQ=Łš$\frac{4\sqrt{3}}{3}$+$\frac{2\sqrt{3}}{3}$tŁ©cmŁŹ
ĄàS=$\frac{1}{2}$AP•AQ=$\frac{1}{2}$Łš2t-4Ł©Łš$\frac{4\sqrt{3}}{3}$+$\frac{2\sqrt{3}}{3}$tŁ©=Łš$\frac{2\sqrt{3}}{3}$t2-$\frac{8\sqrt{3}}{3}$Ł©cm2Łź
”ăÆÀ ŽËÌâÊôÓÚÏàËÆĐÎŚÛșÏÌ⣏É挰”ÄÖȘʶÓĐŁșÏàËÆÈęœÇĐΔÄĆжšÓëĐÔÖÊŁŹÈ«”ÈÈęœÇĐΔÄĆжšÓëĐÔÖÊŁŹÒÔŒ°čŽčɶšÀíŁŹÀûÓĂÁË·ÖÀàÌÖÂÛ”ÄËŒÏ룏ÊìÁ·ŐÆÎŐÏàËÆÈęœÇĐΔÄĆжšÓëĐÔÖÊÊǜⱟÌâ”ÄčŰŒüŁź


 »„¶ŻżÎÌĂÏ”ÁĐŽđ°ž
»„¶ŻżÎÌĂÏ”ÁĐŽđ°ž
| Äꌶ | žßÖĐżÎłÌ | Äꌶ | łőÖĐżÎłÌ |
| žßÒ» | žßÒ»Ăâ·ŃżÎłÌÍÆŒöŁĄ | łőÒ» | łőÒ»Ăâ·ŃżÎłÌÍÆŒöŁĄ |
| žß¶ț | žß¶țĂâ·ŃżÎłÌÍÆŒöŁĄ | łő¶ț | łő¶țĂâ·ŃżÎłÌÍÆŒöŁĄ |
| žßÈę | žßÈęĂâ·ŃżÎłÌÍÆŒöŁĄ | łőÈę | łőÈęĂâ·ŃżÎłÌÍÆŒöŁĄ |
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁșŃĄÔńÌâ
| AŁź | 1-$\frac{x}{6}=\frac{1-x}{2}$ | BŁź | 2Łšx-3Ł©=-x+1 | CŁź | 2x+1=3x-1 | DŁź | 3Łš1-2xŁ©-2Łšx+2Ł©=0 |
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁșœâŽđÌâ
 ÈçÍŒŁŹÒ»ŽÎșŻÊęy=-$\frac{2}{3}$x+m”ÄÍŒÏóÓëxÖ᜻ÓÚ”ăAŁš3ŁŹ0Ł©ŁŹÓëyÖ᜻ÓÚ”ăBŁź
ÈçÍŒŁŹÒ»ŽÎșŻÊęy=-$\frac{2}{3}$x+m”ÄÍŒÏóÓëxÖ᜻ÓÚ”ăAŁš3ŁŹ0Ł©ŁŹÓëyÖ᜻ÓÚ”ăBŁźČ鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁșœâŽđÌâ
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁșÌîżŐÌâ
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁșœâŽđÌâ
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁșŃĄÔńÌâ
 ÈçÍŒŁŹÒÔRtĄśABC”Äб±ßBCÎȘÒ»±ßÔÚĄśABC”ÄÍŹČàŚśŐę·œĐÎBCEFŁŹÉèŐę·œĐΔÄÖĐĐÄÎȘOŁŹÁŹœáAOŁŹÈçčûAB=2ŁŹAO=3$\sqrt{2}$ŁŹÔòtanĄÏAOB”ÄÖ”ÎȘŁšĄĄĄĄŁ©
ÈçÍŒŁŹÒÔRtĄśABC”Äб±ßBCÎȘÒ»±ßÔÚĄśABC”ÄÍŹČàŚśŐę·œĐÎBCEFŁŹÉèŐę·œĐΔÄÖĐĐÄÎȘOŁŹÁŹœáAOŁŹÈçčûAB=2ŁŹAO=3$\sqrt{2}$ŁŹÔòtanĄÏAOB”ÄÖ”ÎȘŁšĄĄĄĄŁ©| AŁź | $\frac{1}{2}$ | BŁź | $\frac{1}{3}$ | CŁź | $\frac{1}{4}$ | DŁź | $\frac{1}{5}$ |
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁșÌîżŐÌâ
Č鿎Žđ°žșÍœâÎö>>
°Ù¶ÈÖÂĐĆ - Á·Ï°ČáÁбí - ÊÔÌâÁбí
șț±±ÊĄ»„ÁȘÍű΄·šșÍČ»ÁŒĐĆÏąŸÙ±šÆœÌš | ÍűÉÏÓĐșŠĐĆÏąŸÙ±šŚšÇű | ”çĐĆŐ©ÆŸÙ±šŚšÇű | ÉæÀúÊ·ĐéÎȚÖśÒćÓĐșŠĐĆÏąŸÙ±šŚšÇű | ÉæÆóÇÖÈšŸÙ±šŚšÇű
΄·šșÍČ»ÁŒĐĆÏąŸÙ±š”ç»°Łș027-86699610 ŸÙ±šÓÊÏäŁș58377363@163.com