
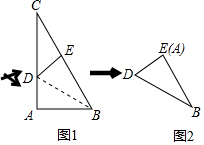
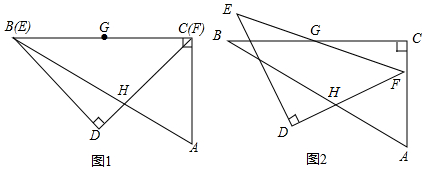
 在三角形纸片ABC中,∠A=90°,∠C=30°,AC=30cm,将该纸片沿过点B的直线折叠,使点A落在斜边BC上的一点E处,折痕记为BD(如图1),减去△CDE后得到双层△BDE(如图2),再沿着过△BDE某顶点的直线将双层三角形剪开,使得展开后的平面图形中有一个是平行四边形,则所得平行四边形的周长为40或$\frac{80\sqrt{3}}{3}$cm.
在三角形纸片ABC中,∠A=90°,∠C=30°,AC=30cm,将该纸片沿过点B的直线折叠,使点A落在斜边BC上的一点E处,折痕记为BD(如图1),减去△CDE后得到双层△BDE(如图2),再沿着过△BDE某顶点的直线将双层三角形剪开,使得展开后的平面图形中有一个是平行四边形,则所得平行四边形的周长为40或$\frac{80\sqrt{3}}{3}$cm. 分析 解直角三角形得到AB=10$\sqrt{3}$,∠ABC=60°,根据折叠的性质得到∠ABD=∠EBD=$\frac{1}{2}∠$ABC=30°,BE=AB=10$\sqrt{3}$,求得DE=10,BD=20,如图1,平行四边形的边是DF,BF,如图2,平行四边形的边是DE,EG,于是得到结论.
解答 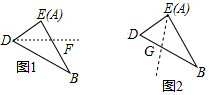 解:∵∠A=90°,∠C=30°,AC=30cm,
解:∵∠A=90°,∠C=30°,AC=30cm,
∴AB=10$\sqrt{3}$,∠ABC=60°,
∵△ADB≌△EDB,
∴∠ABD=∠EBD=$\frac{1}{2}∠$ABC=30°,BE=AB=10$\sqrt{3}$,
∴DE=10,BD=20,
如图1,平行四边形的边是DF,BF,且DF=BF=$\frac{20\sqrt{3}}{3}$,
∴平行四边形的周长=$\frac{80\sqrt{3}}{3}$,
如图2,平行四边形的边是DE,EG,且DF=BF=10,
∴平行四边形的周长=40,
综上所述:平行四边形的周长为40或$\frac{80\sqrt{3}}{3}$,
故答案为:40或$\frac{80\sqrt{3}}{3}$.
点评 本题考查了剪纸问题,平行四边形的性质,解直角三角形,正确的理解题意是解题的关键.


 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
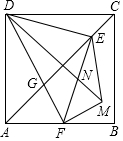 如图,正方形ABCD中,AD=4,点E是对角线AC上一点,连接DE,过点E作EF⊥ED,交AB于点F,连接DF,交AC于点G,将△EFG沿EF翻折,得到△EFM,连接DM,交EF于点N,若点F是AB边的中点,则△EMN的周长是$\frac{{5\sqrt{2}+\sqrt{10}}}{2}$.
如图,正方形ABCD中,AD=4,点E是对角线AC上一点,连接DE,过点E作EF⊥ED,交AB于点F,连接DF,交AC于点G,将△EFG沿EF翻折,得到△EFM,连接DM,交EF于点N,若点F是AB边的中点,则△EMN的周长是$\frac{{5\sqrt{2}+\sqrt{10}}}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
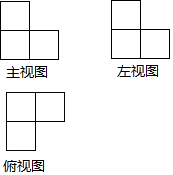 一个由完全相同的小正方体组成的几何体三视图如图所示,若在这个几何体的基础上增加几个相同的小正方体,将其补成一个大正方体,则需要增加的小正方体的最少个数为( )
一个由完全相同的小正方体组成的几何体三视图如图所示,若在这个几何体的基础上增加几个相同的小正方体,将其补成一个大正方体,则需要增加的小正方体的最少个数为( )| A. | 4 | B. | 3 | C. | 6 | D. | 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
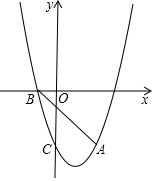 如图,抛物线y=ax2+bx-3经过点A(2,-3),与x轴负半轴交于点B,与y轴交于点C,且OC=3OB.
如图,抛物线y=ax2+bx-3经过点A(2,-3),与x轴负半轴交于点B,与y轴交于点C,且OC=3OB.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2 | B. | 4 | C. | 8 | D. | 不确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{2}}}{2}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $\sqrt{2}$ | D. | $\sqrt{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com