
ΓΨΧβΡΩΓΩ–ΓΕ§”κ–ΓœΡ «Ρ≥÷–―ßάΚ«ρΕ”ΒΡΕ”‘±Θ§‘ΎΉνΫϋΈε≥Γ«ρ»ϋ÷–ΒΡΒΟΖ÷»γœ¬±μΥυ ΨΘΚ
ΒΎ“Μ≥Γ | ΒΎΕΰ≥Γ | ΒΎ»ΐ≥Γ | ΒΎΥΡ≥Γ | ΒΎΈε≥Γ | |
–ΓΕ§ | 10 | 13 | 9 | 8 | 10 |
–ΓœΡ | 12 | 2 | 13 | 21 | 2 |
Θ®1Θ©ΗυΨί…œ±μΥυΗχΒΡ ΐΨίΘ§Χν–¥œ¬±μΘΚ
ΤΫΨυ ΐ | ÷–ΈΜ ΐ | ÷Ύ ΐ | ΖΫ≤ν | |
–ΓΕ§ | 10 | 10 | 2Θ°8 | |
–ΓœΡ | 10 | 12 | 32Θ°4 |
Θ®2Θ©ΗυΨί“‘…œ–≈œΔΘ§»τΫΧΝΖ―Γ‘ώ–ΓΕ§≤ΈΦ”œ¬“Μ≥Γ±»»ϋΘ§ΫΧΝΖΒΡάμ”… « ≤Ο¥ΘΩ
Θ®3Θ©»τ–ΓΕ§ΒΡœ¬“Μ≥Γ«ρ»ϋΒΟΖ÷ «11Ζ÷Θ§‘ρ‘Ύ–ΓΕ§ΒΟΖ÷ΒΡΥΡΗωΆ≥ΦΤΝΩ÷–Θ®ΤΫΨυ ΐΓΔ÷–ΈΜ ΐΓΔ÷Ύ ΐ”κΖΫ≤νΘ©ΡΡ–©ΖΔ…ζΝΥΗΡ±δΘ§ΗΡ±δΚσ «±δ¥σΜΙ «±δ–ΓΘΩΘ®÷Μ“ΣΜΊ¥π «ΓΑ±δ¥σΓ±ΜρΓΑ±δ–ΓΓ±Θ©
Θ®![]() Θ©
Θ©
ΓΨ¥πΑΗΓΩΘ®1Θ©÷–ΈΜ ΐΈΣ10ΘΜ÷Ύ ΐΈΣ2ΘΜΘ®2Θ©–ΓΕ§ΒΡΒΟΖ÷Έ»Ε®Θ§Ρή’ΐ≥ΘΖΔΜ”ΘΜΘ®3Θ©ΤΫΨυ ΐ±δ¥σΘ§ΖΫ≤ν±δ–Γ
ΓΨΫβΈωΓΩ
Θ®1Θ©ΫΪ–ΓΕ§ΒΡ≥…Φ®Α¥’’¥”¥σΒΫ–Γ÷Ί–¬≈≈Ν–Φ¥Ω…ΒΟΒΫ÷–ΈΜ ΐΘ§–ΓœΡΒΡ≥…Φ®÷–≥ωœ÷¥Έ ΐΉνΕύΒΡ ΐΦ¥ «÷Ύ ΐΘΜ
Θ®2Θ©ΗυΨί±μΗώΖ÷Έω–ΓΕ§”κ–ΓœΡΒΡΗςœν≥…Φ®Θ§Φ¥Ω…ΒΟΒΫ¥πΑΗΘΜ
Θ®3Θ©±δΜ·ΒΡ”Π «ΤΫΨυ ΐΚΆΖΫ≤νΘ§‘≠ά¥ΒΡΤΫΨυ ΐ «10Θ§‘ωΦ”ΒΟΖ÷11ΚσΤΫΨυ ΐ”Π «‘ω¥σΘ§ΖΫ≤ν±δ–ΓΝΥ.
ΫβΘΚΘ®1Θ©–ΓΕ§Ης≥ΓΒΟΖ÷”…¥σΒΫ–Γ≈≈Ν–ΈΣΘΚ13Θ§10Θ§10Θ§9Θ§8ΘΜ”Ύ «÷–ΈΜ ΐΈΣ10ΘΜ
–ΓœΡΗς≥ΓΒΟΖ÷÷–Θ§≥ωœ÷¥Έ ΐΉνΕύΒΡΒΟΖ÷ΈΣΘΚ2ΘΜ”Ύ «÷Ύ ΐΈΣ2Θ§
Ι ¥πΑΗΈΣΘΚ10Θ§2ΘΜ
Θ®2Θ©ΫΧΝΖ―Γ‘ώ–ΓΕ§≤ΈΦ”œ¬“Μ≥Γ±»»ϋΒΡάμ”…ΘΚ–ΓΕ§”κ–ΓœΡΤΫΨυΒΟΖ÷œύΆ§Θ§–ΓΕ§ΒΡΖΫ≤ν–Γ”Ύ–ΓœΡΘ§Φ¥–ΓΕ§ΒΡΒΟΖ÷Έ»Ε®Θ§Ρή’ΐ≥ΘΖΔΜ”Θ°
Θ®3Θ©‘Ό±»“Μ≥ΓΘ§–ΓΕ§ΒΡΒΟΖ÷«ιΩω¥”¥σΒΫ–Γ≈≈Ν–ΈΣ13Θ§11Θ§10Θ§10Θ§9Θ§8ΘΜ
ΤΫΨυ ΐΘΚ![]() Θ®13+11+10+10+9+8Θ©ΘΫ
Θ®13+11+10+10+9+8Θ©ΘΫ![]() ΘΜ
ΘΜ
÷–ΈΜ ΐΘΚ10ΘΜ
÷Ύ ΐΘΚ10ΘΜ
ΖΫ≤νΘΚS2ΘΫ![]() [Θ®13©¹
[Θ®13©¹![]() Θ©2+Θ®11©¹
Θ©2+Θ®11©¹![]() Θ©2+Θ®10©¹
Θ©2+Θ®10©¹![]() Θ©2+Θ®10©¹
Θ©2+Θ®10©¹![]() Θ©2+Θ®9©¹
Θ©2+Θ®9©¹![]() Θ©2+Θ®8©¹
Θ©2+Θ®8©¹![]() Θ©2Γ÷2Θ°47Θ°
Θ©2Γ÷2Θ°47Θ°
Ω…ΦϊΘ§ΤΫΨυ ΐ±δ¥σΘ§ΖΫ≤ν±δ–ΓΘ°


 ΆθΚσ–έ―ßΑΗΫΧ≤ΡΆξ»ΪΫβΕΝœΒΝ–¥πΑΗ
ΆθΚσ–έ―ßΑΗΫΧ≤ΡΆξ»ΪΫβΕΝœΒΝ–¥πΑΗ ΚΘΒμΩΈ ±–¬Ής“ΒΫπΑώΨμœΒΝ–¥πΑΗ
ΚΘΒμΩΈ ±–¬Ής“ΒΫπΑώΨμœΒΝ–¥πΑΗ
| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§ «”…8Ηω¥σ–ΓœύΆ§ΒΡ–Γ’ΐΖΫΧεΉιΚœ≥…ΒΡΦρΒΞΦΗΚΈΧεΘ°
Θ®1Θ©ΗΟΦΗΚΈΧεΒΡ÷ς ”ΆΦ»γΆΦΥυ ΨΘ§«κ‘Ύœ¬ΟφΖΫΗώ÷Ϋ÷–Ζ÷±πΜ≠≥ωΥϋΒΡΉσ ”ΆΦΚΆΗ© ”ΆΦΘΜΘ®±ΏΩρœΏΦ”¥÷Μ≠≥ωΘ§≤ΔΆΩ…œ“θ”ΑΘ©
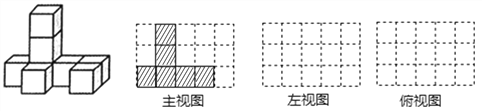
Θ®2Θ©»γΙϊ‘Ύ’βΗωΦΗΚΈΧε…œ‘ΌΧμΦ”“Μ–©œύΆ§ΒΡ–Γ’ΐΖΫΧεΘ§≤Δ±Θ≥÷’βΗωΦΗΚΈΧεΒΡΗ© ”ΆΦΚΆ÷ς ”ΆΦ≤Μ±δΘ§Ρ«Ο¥«κ‘Ύœ¬Ν–ΆχΗώΆΦ÷–Μ≠≥ωΧμΦ”–Γ’ΐΖΫΧεΚσΥυΒΟΦΗΚΈΧεΥυ”–Ω…ΡήΒΡΉσ ”ΆΦΘ°

≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“Μ¥ΈΚ· ΐy=©¹kx+k”κΖ¥±»άΐΚ· ΐy=©¹![]() Θ®kΓΌ0Θ©‘ΎΆ§“ΜΉχ±ξœΒ÷–ΒΡΆΦœσΩ…Ρή «Θ®ΓΓΓΓΘ©
Θ®kΓΌ0Θ©‘ΎΆ§“ΜΉχ±ξœΒ÷–ΒΡΆΦœσΩ…Ρή «Θ®ΓΓΓΓΘ©
A.  B.
B. 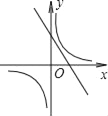 C.
C.  D.
D. 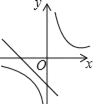
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘Ύ![]() ÷–Θ§
÷–Θ§![]() ΚΆ
ΚΆ![]() ΒΡΤΫΖ÷œΏœύΫΜ”ΎΒψ
ΒΡΤΫΖ÷œΏœύΫΜ”ΎΒψ![]() Θ§ΙΐΒψ
Θ§ΙΐΒψ![]() Ής
Ής![]() ΫΜ
ΫΜ![]() ”ΎΒψ
”ΎΒψ![]() Θ§ΫΜ
Θ§ΫΜ![]() ”ΎΒψ
”ΎΒψ![]() Θ§ΙΐΒψ
Θ§ΙΐΒψ![]() Ής
Ής![]() ”ΎΒψ
”ΎΒψ![]() Θ§œ¬Ν–ΥΡΗωΫα¬έΘΚ
Θ§œ¬Ν–ΥΡΗωΫα¬έΘΚ
ΔΌ![]() ΘΜΔΎ
ΘΜΔΎ![]() ΘΜ
ΘΜ
ΔέΒψ![]() ΒΫ
ΒΫ![]() Ης±ΏΒΡΨύάκœύΒ»ΘΜΔέ…η
Ης±ΏΒΡΨύάκœύΒ»ΘΜΔέ…η![]() Θ§
Θ§![]() Θ§‘ρ
Θ§‘ρ![]() Θ°
Θ°
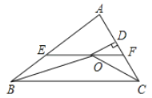
Τδ÷–’ΐ»ΖΒΡΫα¬έ «__________Θ°Θ®ΧνΥυ”–’ΐ»ΖΫα¬έΒΡ–ρΚ≈Θ©
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§“―÷ΣABΓΆBCΘ§CDΓΆBCΘ§AB=4Θ§CD=2Θ°PΈΣœΏΕΈBC…œΒΡΒψΘ§…ηBC=mΘ°
Δ≈»τm=9Θ§
ΔΌ»τΓςBAPΓΉΓςCDPΘ§«σœΏΕΈBPΒΡ≥ΛΘΜ
ΔΎ»τΓςBAPΓΉΓςCPDΘ§«σœΏΕΈBPΒΡ≥ΛΘΜ
ΔΤ ‘«σmΈΣΚΈ÷Β ±Θ§ ΙΒΟΓςBAP”κΓςCDPœύΥΤΒΡΒψP”–«“÷Μ”–2ΗωΘ°

≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
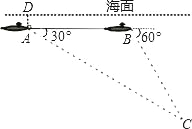
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘ΎA¥Π”–“ΜΥ“«±ΆßΘ§≤Δ≤βΒΟ‘ΎΗ© ”Ϋ«ΈΣ30ΓψΒΡΖΫœρ”–ΚΎœΜΉ”Θ§¥Υ ±«±ΆßΨύΚΘΤΫΟφ500ΟΉΘ§ΦΧ–χ‘ΎΆ§“Μ…νΕ»―Ί÷±œΏΚΫ––3000ΟΉΚσ‘Ό¥Έ‘ΎBΒψ≥ω≤βΒΟΗ© ”Ϋ«ΈΣ60Γψ’ΐ«ΑΖΫΒΡΚΘΒΉΚΎœΜΉ”Θ§«σΚΘΒΉΚΎœΜΉ”Υυ¥ΠΈΜ÷ΟCΒψ≥ωΨύάκΚΘΟφΒΡ…νΕ»Θ°Θ®±ΘΝτΗυΚ≈Θ©
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ Γ…δΜςΕ”ΈΣ¥”ΦΉΓΔ““ΝΫΟϊ‘ΥΕ·‘±÷–―ΓΑΈ“Μ»Υ≤ΈΦ”»ΪΙζ±»»ϋΘ§Ε‘
ΥϊΟ«Ϋχ––ΝΥΝυ¥Έ≤β ‘Θ§≤β ‘≥…Φ®»γœ¬±μΘ®ΒΞΈΜΘΚΜΖΘ©ΘΚ
ΒΎ“Μ¥Έ | ΒΎΕΰ¥Έ | ΒΎ»ΐ¥Έ | ΒΎΥΡ¥Έ | ΒΎΈε¥Έ | ΒΎΝυ¥Έ | |
ΦΉ | 10 | 8 | 9 | 8 | 10 | 9 |
““ | 10 | 7 | 10 | 10 | 9 | 8 |
Θ®1Θ©ΗυΨί±μΗώ÷–ΒΡ ΐΨίΘ§ΦΤΥψ≥ωΦΉΒΡΤΫΨυ≥…Φ® « ΜΖΘ§““ΒΡΤΫΨυ≥…Φ® « ΜΖΘΜ
Θ®2Θ©Ζ÷±πΦΤΥψΦΉΓΔ““Νυ¥Έ≤β ‘≥…Φ®ΒΡΖΫ≤νΘΜ
Θ®3Θ©ΗυΨίΘ®1Θ©ΓΔΘ®2Θ©ΦΤΥψΒΡΫαΙϊΘ§Ρψ»œΈΣΆΤΦωΥ≠≤ΈΦ”»ΪΙζ±»»ϋΗϋΚœ Θ§«κΥΒΟςάμ”…Θ°
Θ®ΦΤΥψΖΫ≤νΒΡΙΪ ΫΘΚs2ΘΫ![]() Θέ
Θέ![]() ΘίΘ©
ΘίΘ©
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§ΥΡ±Ώ–ΈABCD÷–Θ§AB=10Θ§BC=13Θ§CD=12Θ§AD=5Θ§ADΓΆCDΘ§«σΥΡ±Ώ–ΈABCDΒΡΟφΜΐΘ°

≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦ1Θ§‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒ÷–Θ§“Μ¥ΈΚ· ΐy=©¹2x+8ΒΡΆΦœσ”κx÷αΘ§y÷αΖ÷±πΫΜ”ΎΒψAΘ§ΒψCΘ§ΙΐΒψAΉςABΓΆx÷αΘ§¥ΙΉψΈΣΒψAΘ§ΙΐΒψCΉςCBΓΆy÷αΘ§¥ΙΉψΈΣΒψCΘ§ΝΫΧθ¥ΙœΏœύΫΜ”ΎΒψBΘ°

Θ®1Θ©œΏΕΈABΘ§BCΘ§ACΒΡ≥ΛΖ÷±πΈΣAB=ΓΓ ΓΓΘ§BC=ΓΓ ΓΓΘ§AC=ΓΓ ΓΓΘΜ
Θ®2Θ©’έΒΰΆΦ1÷–ΒΡΓςABCΘ§ ΙΒψA”κΒψC÷ΊΚœΘ§‘ΌΫΪ’έΒΰΚσΒΡΆΦ–Έ’ΙΩΣΘ§’έΚέDEΫΜAB”ΎΒψDΘ§ΫΜAC”ΎΒψEΘ§Ν§Ϋ”CDΘ§»γΆΦ2Θ°
«κ¥”œ¬Ν–AΓΔBΝΫΧβ÷–»Έ―Γ“ΜΧβΉς¥πΘ§Έ“―Γ‘ώΓΓ ΓΓΧβΘ°
AΘΚΔΌ«σœΏΕΈADΒΡ≥ΛΘΜ
ΔΎ‘Ύy÷α…œΘ§ «Ζώ¥φ‘ΎΒψPΘ§ ΙΒΟΓςAPDΈΣΒ»―ϋ»ΐΫ«–ΈΘΩ»τ¥φ‘ΎΘ§«κ÷±Ϋ”–¥≥ωΖϊΚœΧθΦΰΒΡΥυ”–ΒψPΒΡΉχ±ξΘΜ»τ≤Μ¥φ‘ΎΘ§«κΥΒΟςάμ”…Θ°
BΘΚΔΌ«σœΏΕΈDEΒΡ≥ΛΘΜ
ΔΎ‘ΎΉχ±ξΤΫΟφΡΎΘ§ «Ζώ¥φ‘ΎΒψPΘ®≥ΐΒψBΆβΘ©Θ§ ΙΒΟ“‘ΒψAΘ§PΘ§CΈΣΕΞΒψΒΡ»ΐΫ«–Έ”κΓςABC»ΪΒ»ΘΩ»τ¥φ‘ΎΘ§«κ÷±Ϋ”–¥≥ωΥυ”–ΖϊΚœΧθΦΰΒΡΒψPΒΡΉχ±ξΘΜ»τ≤Μ¥φ‘ΎΘ§«κΥΒΟςάμ”…Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΑΌΕ»÷¬–≈ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com