
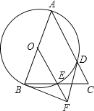
【题目】已知,如图,在![]() 中,
中,![]() ,以
,以![]() 为直径作
为直径作![]() 分别交
分别交![]() ,
,![]() 于
于![]() ,
,![]() 两点,过
两点,过![]() 点的切线交
点的切线交![]() 的延长线于点
的延长线于点![]() .下列结论:
.下列结论:
①![]() ;②两段劣弧
;②两段劣弧![]() =
=![]() ;③
;③![]() 与
与![]() 相切;④
相切;④![]() .
.
其中一定正确的有( )个.
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】C
【解析】
①由等腰三角形性质得到∠OEB=∠ABC=∠ACB,从而可得OE∥AC;
②连接OD,由平行线的性质和等腰三角形的性质证得∠BOE=∠EOD,从而得到![]() =
=![]() ;
;
③由SAS证得△OBF≌△ODF,即可得到∠OBF=∠ODF.根据切线的性质可得∠OBF=90°,则有∠ODF=90°,即可得到DF与⊙O相切;
④由OE∥AC,得出△BOE∽△BAC,根据相似三角形的性质即可得到![]() =(
=(![]() )2=
)2=![]() ,△BDE的面积≠△BOE的面积,得出④不一定正确,即可得出结论.
,△BDE的面积≠△BOE的面积,得出④不一定正确,即可得出结论.
①∵AB=AC,OB=OE,∴∠ABC=∠ACB,∠OBE=∠OEB,∴∠OEB=∠ACB,∴OE∥AC,故①正确;
②连接OD,如图所示:
∵OE∥AC,∴∠BOE=∠OAD,∠EOD=∠ADO.
∵OA=OD,∴∠OAD=∠ODA,∴∠BOE=∠EOD,∴![]() =
=![]() ,故②正确;
,故②正确;
③在△OBF和△ODF中,∵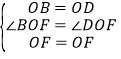 ,∴△OBF≌△ODF(SAS),∴∠OBF=∠ODF.
,∴△OBF≌△ODF(SAS),∴∠OBF=∠ODF.
∵BF与⊙O相切于点B,∴∠OBF=90°,∴∠ODF=90°,∴DF与⊙O相切,故③正确;
④∵OE∥AC,∴△BOE∽△BAC,∴![]() =(
=(![]() )2=(
)2=(![]() )2=
)2=![]() ,而△BDE的面积≠△BOE的面积,故④不正确;正确的有3个.
,而△BDE的面积≠△BOE的面积,故④不正确;正确的有3个.
故选C.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点D在AB边上,DE∥BC,与边AC交于点E,连结BE.记△ADE,△BCE的面积分别为S1,S2,( )
A. 若2AD>AB,则3S1>2S2 B. 若2AD>AB,则3S1<2S2
C. 若2AD<AB,则3S1>2S2 D. 若2AD<AB,则3S1<2S2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,矩形OABC的顶点O与坐标原点重合,A、C分别在坐标轴上,点B的坐标为(4,2),直线![]() 交AB,BC分别于点M,N,反比例函数
交AB,BC分别于点M,N,反比例函数![]() 的图象经过点M,N.
的图象经过点M,N.
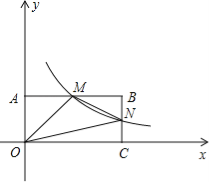
(1)求反比例函数的解析式;
(2)若点P在y轴上,且△OPM的面积与四边形BMON的面积相等,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() ,
,![]() 与
与![]() 和
和![]() 分别相切于点
分别相切于点![]() 和点
和点![]() .点
.点![]() 和点
和点![]() 分别是
分别是![]() 和
和![]() 上的动点,
上的动点,![]() 沿
沿![]() 和
和![]() 平移.
平移.![]() 的半径为
的半径为![]() ,
,![]() .下列结论错误的是( )
.下列结论错误的是( )
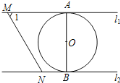
A. ![]() B.
B. ![]() 和
和![]() 的距离为
的距离为![]()
C. 若![]() ,则
,则![]() 与
与![]() 相切 D. 若
相切 D. 若![]() 与
与![]() 相切,则
相切,则![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,点E,F分别在AB,CD上,且![]() ,连接EF交BD于点O连接AO.若
,连接EF交BD于点O连接AO.若![]() ,,则
,,则![]() 的度数为( )
的度数为( )
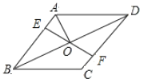
A.50°B.55°C.65°D.75°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为决定谁获得仅有的一张电影票,甲和乙设计了如下游戏:在三张完全相同的卡片上,分别写上字母![]() ,
,![]() ,
,![]() ,背面朝上,每次活动洗均匀.
,背面朝上,每次活动洗均匀.
甲说:我随机抽取一张,若抽到字母![]() ,电影票归我;
,电影票归我;
乙说:我随机抽取一张后放回,再随机抽取一张,若两次抽取的字母相同的电影票归我.
![]() 求甲获得电影票的概率;
求甲获得电影票的概率;![]() 求乙获得电影票的概率;
求乙获得电影票的概率;![]() 此游戏对谁有利?
此游戏对谁有利?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com