
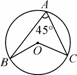
如图,已知圆O的半径为4,∠A=45°,若一个圆锥的侧面展开图与扇形OBC能完全重合,则该圆锥的底面圆的半径为________.
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:初中数学 来源: 题型:
如图15,从一个直径为4的圆形铁片中剪下一个圆心角为90°的扇形ABC.
(1)求这个扇形的面积;
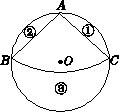
(2)在剩下的材料中,能否从③中剪出一个圆作为底面,与扇形ABC围成一个圆锥?若不能,请说明理由;若能,请求出剪的圆的半径是多少.
查看答案和解析>>
科目:初中数学 来源: 题型:
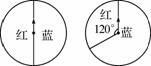
用图中两个相可自由转动的转盘做“配紫色”游戏:分别是旋转两个转盘,若其中一 个转出红色,另一个转出蓝色即可配成紫色那么可配成紫色.的概率是( )
个转出红色,另一个转出蓝色即可配成紫色那么可配成紫色.的概率是( )
A.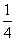

 B.
B.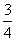 C.
C.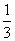 D.0.5
D.0.5
查看答案和解析>>
科目:初中数学 来源: 题型:
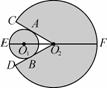
某玩具由一个圆形区域和一个扇形区域组成.如图,在⊙O1和扇形O2CD中,⊙O1与O2C、O2D分别相切于点A、B.已知∠CO2D=60°,E、F是直线O1O2与⊙O1、扇形O2CD的两个交点,且EF=24 cm,⊙O1的半径为x cm .
.
(1)用含x的代数式表示扇形O2CD的半径;
(2)若⊙O1和扇形O2CD两个区域的制作成本分别为0.45元/cm2和0.06元/cm2,当⊙O1的半径为多少时,该玩具的制作成本最小?
查看答案和解析>>
科目:初中数学 来源: 题型:
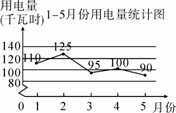
小林家今年1~5月份的用电量情况如图所示 .由图可知,相邻两个月中,用电量变化最大的是( )
.由图可知,相邻两个月中,用电量变化最大的是( )
A.1月至2月 B.2月至3月 C.3月至4月 D.4月至5月
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com