
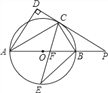
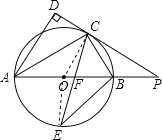
【题目】如图,AB是⊙O的直径,点C是⊙O上一点,AD和过点C的切线互相垂直,垂足为D,直线DC与AB的延长线相交于P.弦CE平分∠ACB,交直径AB于点F,连结BE.
(1)求证:AC平分∠DAB;
(2)探究线段PC,PF之间的大小关系,并加以证明;
(3)若tan∠PCB=![]() ,BE=
,BE=![]() ,求PF的长.
,求PF的长.
【答案】(1)见解析;(2)PC=PF.证明见解析;(3)![]() .
.
【解析】试题分析:(1)、连接OC,根据切线的性质得出∠OCP=∠D=90°即 OC∥AD,然后根据OA=OC得出∠CAD=∠OCA=∠OAC,从而得出角平分线;(2)、根据∠PCB+∠ACD=∠CAD+∠ACD=90°,从而得出∠CAB=∠CAD=∠PCB,结合∠ACE=∠BCE,∠PFC=∠CAB+∠ACE,∠PCF=∠PCB+∠BCE得出∠PFC=∠PCF,从而得出答案;(3)、连接AE,根据题意得出△PCB和△PAC相似,然后设PB=3x,则PC=4x,根据Rt△POC的勾股定理得出x的值,从而得出答案.
试题解析:(1)连接OC. ∵OA=OC,∴∠OAC=∠OCA.
∵PC是⊙O的切线,AD⊥CD, ∴∠OCP=∠D=90°, ∴ OC∥AD.
∴ ∠CAD=∠OCA=∠OAC.即AC平分∠DAB.
(2)PC=PF.
证明:∵AB是直径, ∴∠ACB=90°,∴∠PCB+∠ACD=90° 又∵∠CAD+∠ACD=90°,
∴∠CAB=∠CAD=∠PCB.
又∵∠ACE=∠BCE,∠PFC=∠CAB+∠ACE,∠PCF=∠PCB+∠BCE. ∴∠PFC=∠PCF.
∴PC=PF.
(3)连接AE. ∵∠ACE=∠BCE,∴![]() =
=![]() , ∴AE=BE.
, ∴AE=BE.
又∵AB是直径, ∴∠AEB=90°.AB=![]() , ∴OB=OC=5.
, ∴OB=OC=5.
∵∠PCB=∠PAC,∠P=∠P, ∴△PCB∽△PAC. ∴![]() .
.
∵tan∠PCB=tan∠CAB=![]() , ∴
, ∴![]() =
=![]() .
.
设PB=3x,则PC=4x,在Rt△POC中,(3x+5)2=(4x)2+52,
解得x1=0,![]() . ∵x>0,∴
. ∵x>0,∴![]() , ∴PF=PC=
, ∴PF=PC=![]() .
.


科目:初中数学 来源: 题型:
【题目】华联超市购进一批四阶魔方,按进价提高40%后标价,为了让利于民,增加销量,超市决定打八折出售,这时每个魔方的售价为28元.
(1)求魔方的进价?
(2)超市卖出一半后,正好赶上双十一促销,商店决定将剩下的魔方以每3个80元的价格出售,很快销售一空,这批魔方超市共获利2800元,求该超市共购进魔方多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某校七年级男生的身高(单位:![]() )情况,随机抽取了七年级部分学生进行了抽样调查.统计数据如下表:
)情况,随机抽取了七年级部分学生进行了抽样调查.统计数据如下表:
组别 |
|
|
|
|
|
身高 |
|
|
|
|
|
人数 |
|
|
|
|
|
(1)样本容量是多少?组距是多少?组数是多少?
(2)画出适当的统计图表示上面的信息;
(3)若全校七年级学生有![]() 人,请估计身高不低于
人,请估计身高不低于![]() 的学生人数.
的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市今年中考理化实验操作考试,采用学生抽签方式决定自己的考试内容.规定:每位考生必须在三个物理实验(用纸签A、B、C表示)和三个化学实验(用纸签D、E、F表示)中各抽取一个进行考试,小刚在看不到纸签的情况下,分别从中各随机抽取一个.
(1) 用“列表法”或“树状图法”表示所有可能出现的结果;
(2) 小刚抽到物理实验B和化学实验F(记作事件P)的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
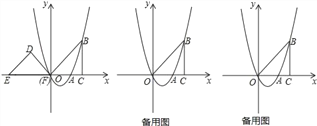
【题目】如图,抛物线y=ax2+bx(a≠0)经过点A(2,0),点B(3,3),BC⊥x轴于点C,连接OB,等腰直角三角形DEF的斜边EF在x轴上,点E的坐标为(﹣4,0),点F与原点重合
(1)求抛物线的解析式并直接写出它的对称轴;
(2)△DEF以每秒1个单位长度的速度沿x轴正方向移动,运动时间为t秒,当点D落在BC边上时停止运动,设△DEF与△OBC的重叠部分的面积为S,求出S关于t的函数关系式;
(3)点P是抛物线对称轴上一点,当△ABP是直角三角形时,请直接写出所有符合条件的点P坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
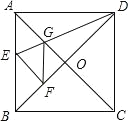
【题目】如图,在正方形纸片ABCD中,对角线AC、BD交于点O,折叠正方形纸片ABCD,使AD落在BD上,点A恰好与BD上的点F重合,展开后,折叠DE分别交AB、AC于E、G,连接GF,下列结论:①∠FGD=112.5°②BE=2OG③S△AGD=S△OGD④四边形AEFG是菱形( )
A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
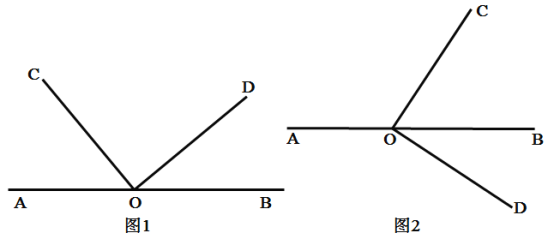
【题目】如图,点O是直线AB上的一点,OD⊥OC,过点O作射线OE平分∠BOC.
(1)如图1,如果∠AOC=50°,依题意补全图形,写出求∠DOE度数的思路(不需要写出完整的推理过程);
(2)当OD绕点O顺时针旋转一定的角度得到图2,使得直角边OC在直线AB的上方,若∠AOC=α,其他条件不变,依题意补全图形,并求∠DOE的度数(用含α的代数式表示);
(3)当OD绕点O继续顺时针旋转一周,回到图1的位置,在旋转过程中你发现∠AOC与∠DOE(0°≤∠AOC≤180°,0°≤∠DOE≤180°)之间有怎样的数量关系?请直接写出你的发现.
查看答案和解析>>
科目:初中数学 来源: 题型:
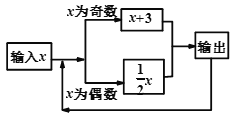
【题目】如图,是某一计算程序,回答如下问题:
(1)当输入某数后,第一次得到的结果为5,则输入的数值x=_______;
(2)若输入的x的值为16时,第1次得到的结果为8,第2次得到的结果为4,…,则第2019次得到的结果是_______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com