
分析 (1)设每头大牛1天约需饲料xkg,每头小牛1天约需饲料ykg,根据题意列出方程组,求出方程组的解得到x与y的值;
(2)设这次购买的牛中大牛有z只,根据不等关系:使牛的数量增加到100只,每天的饲料费用不超过1200元,列出不等式求解即可.
解答 解:(1)设每头大牛1天用饲料xkg,每头小牛1天用饲料ykg,
根据题意得:$\left\{\begin{array}{l}{30x+15y=675}\\{42x+20y=940}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=20}\\{y=5}\end{array}\right.$.
故每头大牛1天用饲料20kg,每头小牛1天用饲料5kg.
(2)设这次购买的牛中大牛有z只,根据题意得:
20×0.8(42+z)+5×0.8(100-42-z)≤1200,
解得z≤24$\frac{2}{3}$,
∵z为整数,
∴这次购买的牛中大牛最多有24只.
点评 此题考查了一元一次不等式的应用,二元一次方程组的应用,找出题中的等量关系和不等关系是解本题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
 如图,直线y=ax+b(a≠0)与双曲线y=$\frac{k}{x}$(k≠0)交于一、三象限内的A,B两点与x轴交于点C,点A的坐标为(2,m),点B的坐标为(n,-2),tan∠BOC=$\frac{2}{5}$.
如图,直线y=ax+b(a≠0)与双曲线y=$\frac{k}{x}$(k≠0)交于一、三象限内的A,B两点与x轴交于点C,点A的坐标为(2,m),点B的坐标为(n,-2),tan∠BOC=$\frac{2}{5}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
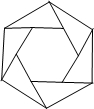 如图,把正六边形各边按同一方向延长,使延长的线段与原正六边形的边长相等,顺次连接这六条线段外端点可以得到一个新的正六边形,…,重复上述过程,经过2018次后,所得到的正六边形边长是原正六边形边长的( )
如图,把正六边形各边按同一方向延长,使延长的线段与原正六边形的边长相等,顺次连接这六条线段外端点可以得到一个新的正六边形,…,重复上述过程,经过2018次后,所得到的正六边形边长是原正六边形边长的( )| A. | ($\sqrt{2}$)2016倍 | B. | ($\sqrt{3}$)2017倍 | C. | ($\sqrt{3}$)2018倍 | D. | ($\sqrt{2}$)2019倍 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
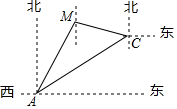 一渔船在海岛A北偏东30°方向的M处遇险,渔船将险情报告给位于A处的救援船后,沿南偏东75°方向向海岛C靠近,同时,从A处出发的救援船沿北偏东60°方向以每小时40$\sqrt{2}$海里的速度匀速航行,30分钟后,救援船在海岛C处恰好追上渔船,那么渔船遇险M处与海岛C的距离是多少海里?($\sqrt{2}$≈1.4,$\sqrt{3}$≈1.7,$\sqrt{6}$≈2.4)
一渔船在海岛A北偏东30°方向的M处遇险,渔船将险情报告给位于A处的救援船后,沿南偏东75°方向向海岛C靠近,同时,从A处出发的救援船沿北偏东60°方向以每小时40$\sqrt{2}$海里的速度匀速航行,30分钟后,救援船在海岛C处恰好追上渔船,那么渔船遇险M处与海岛C的距离是多少海里?($\sqrt{2}$≈1.4,$\sqrt{3}$≈1.7,$\sqrt{6}$≈2.4)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{26}{3}$ | B. | $3\sqrt{2}$ | C. | $\frac{8\sqrt{3}}{3}$或$\frac{14}{3}$ | D. | $\frac{14}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
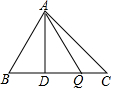 如图所示,△ABC中,已知BC=16,高AD=10,动点Q由C点沿CB向B移动(不与点B重合).设CQ长为x,△ACQ的面积为S,则S与x之间的函数关系式为( )
如图所示,△ABC中,已知BC=16,高AD=10,动点Q由C点沿CB向B移动(不与点B重合).设CQ长为x,△ACQ的面积为S,则S与x之间的函数关系式为( )| A. | S=80-5x | B. | S=5x | C. | S=10x | D. | S=5x+80 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
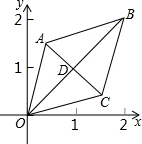 如图,已知菱形OABC的顶点O(0,0),B(2,2),若菱形绕点O逆时针旋转,每秒旋转45°则第30秒时,菱形的对角线交点D的坐标为( )
如图,已知菱形OABC的顶点O(0,0),B(2,2),若菱形绕点O逆时针旋转,每秒旋转45°则第30秒时,菱形的对角线交点D的坐标为( )| A. | (1,-1) | B. | (-1,-1) | C. | ($\sqrt{2}$,0) | D. | (0,-$\sqrt{2}$) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com