
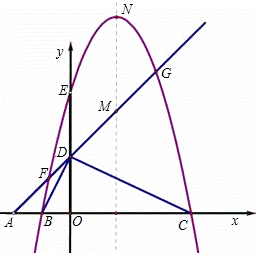
如图11,在平面直角坐标系中,已知点A、B、C在x轴上,点D、E在y轴上,OA=OD=2,OC=OE=4,B为线段OA的中点,直线AD与经过B、E、C三点的抛物线交于F、G两点,与其对称轴交于M,点P为线段FG上一个动点(点P与F、G不重合),作PQ∥y轴与抛物线交于点Q.
(1)求经过B、E、C三点的抛物线的解析式;
(2)判断△BDC的形状,并给出证明;当P在什么位置时,以P、O、C为顶点的三角形是等腰三角形,并求出此时点P的坐标;
(3)若抛物线的顶点为N,连接QN,探究四边形PMNQ的形状:①能否成为菱形;②能否成为等腰梯形?若能,请直接写出点P的坐标;若不能,请说明理由.
解:
(1)B(-1,0)E(0,4)C(4,0)设解析式是y=ax2+bx+c
可得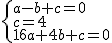 解得
解得
∴y=-x2+3x+4
(2)△BDC是直角三角形
∵BD2=BO2+DO2=5,DC2=DO2+CO2=20,BC2=(BO+CO)2=25
∴BD2+DC2=BC2
∴△BDC是Rt△
∵点A坐标是(-2,0),点D坐标是(0,2)
∴直线AD的解析式是y=x+2
设点P坐标是(x,x+2)
当OP=OC时x2+(x+2)2=16解得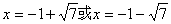 (
(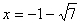 ,舍去)此时点P(
,舍去)此时点P(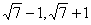 )
)
当PC=OC时(x+2)2+(4-x)2=16方程无解,故不存在
当PO=PC时,点P在OC的中垂线上
∴点P横坐标是2,得点P坐标是(2,4)
∴当△POC是等腰三角形时,点P坐标是(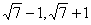 )或(2,4)
)或(2,4)
(3)点M坐标是(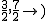 ,点N坐标是(
,点N坐标是(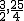 ),∴MN=
),∴MN=
设点P为(x,x+2)Q(x,-x2+3x+4),则PQ=-x2+2x+2
①若PQNM是菱形,则PQ=MN,可得x1=0.5,x2=1.5
当x2=1.5时,点P与点M重合;当x1=0.5时,可求得PM=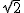 ,此时PM≠ MN所以菱形不存在
,此时PM≠ MN所以菱形不存在
②能成为等腰梯形,此时点P的坐标是(2.5,4.5)


科目:初中数学 来源: 题型:
下面调查中,适合采用全面调查的事件是( ).
A.对全国中学生心理健康现状的调查.
B.对我市食品合格情况的调查.
C.对桂林电视台《桂林板路》收视率的调查.
D.对你所在的班级同学的身高情况的调查.
查看答案和解析>>
科目:初中数学 来源: 题型:
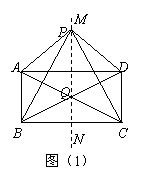
四边形ABCD是矩形,点P是直线AD与BC外的任意一点,连接PA、PB、PC、PD.请解答下列问题:
(1)如图(1),当点P在线段BC的垂直平分线MN上(对角线AC与BD的交点Q除外)时,证明△ PAC
PAC ≌△PDB;
≌△PDB;
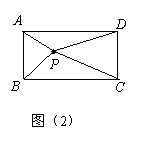
(2)如图(2),当点P在矩形ABCD内部时,求证:PA2+PC2=PB2+PD2;
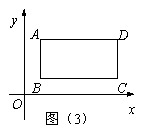
(3)若矩形ABCD在平面直角坐标系xoy中,点B的坐标为(1,1),点D的坐标为(5,3),如图(3)所示,设△PBC的面积为y,△PAD的面积为x,求y与x之间的函数关系式.
 | |||||
 | |||||
 | |||||
查看答案和解析>>
科目:初中数学 来源: 题型:
如图5,某滑板爱好者训练时的斜坡示意图,出于安全因素考虑,决定将训练的斜坡的倾角由45º降为30º,已知原斜坡坡面AB的长为5米,点D、B、C 在同一水平地面上.
(1)改善后斜坡坡面AD比原斜坡坡面AB会加长多少米?(精确到0.01)
(2)若斜坡的正前方能有3米长的空地就能保证安全,已知原斜坡AB的前方有6米长的空地,进行这样的改造是否可行?说明理由。
(参考数据: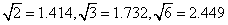 )
)
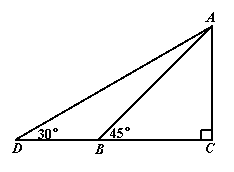 |
图5
查看答案和解析>>
科目:初中数学 来源: 题型:
如图8,直线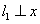 轴于点
轴于点 ,直线
,直线 轴于点
轴于点 ,直线
,直线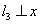 轴于点
轴于点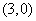 ,…,直线
,…,直线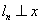 轴于点(n,0)(n为正整数).函数
轴于点(n,0)(n为正整数).函数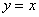 的图象与直线
的图象与直线 ,
,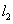 ,
, ,…,
,…,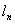 分别交于点
分别交于点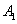 ,
,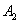 ,
, ,…,
,…,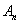 ;函数
;函数 的图象与直线
的图象与直线 ,
,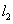 ,
, ,…,
,…,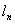 分别交于点
分别交于点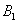 ,
, ,
,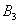 ,…,
,…, .如果
.如果 的面积记作
的面积记作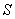 ,四边形
,四边形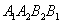 的面积记作
的面积记作 ,四边形
,四边形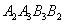 的面积记作
的面积记作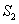 ,…,四边形
,…,四边形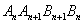 的面积记作
的面积记作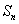 ,
,
 那么
那么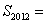 .
.  = .
= .
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,边长为(m+3)的正方形纸片剪出一个边长为m的正方形之后,剩余部分可剪拼成一个矩形(不重叠无缝隙),若拼成的矩形一边长为3,则另一边长是( )
A.m+3 B.m+6
C.2m+3 D.2m+6
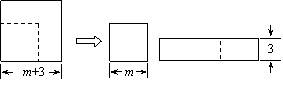
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com