
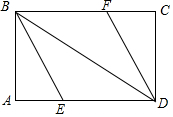
 如图,矩形ABCD中,∠ABD、∠CDB的平分线BE、DF分别交边AD、BC于点E、F.
如图,矩形ABCD中,∠ABD、∠CDB的平分线BE、DF分别交边AD、BC于点E、F.分析 (1)由矩形可得∠ABD=∠CDB,结合BE平分∠ABD、DF平分∠BDC得∠EBD=∠FDB,即可知BE∥DF,根据AD∥BC即可得证;
(2)当∠ABE=30°时,四边形BEDF是菱形,由角平分线知∠ABD=2∠ABE=60°、∠EBD=∠ABE=30°,结合∠A=90°可得∠EDB=∠EBD=30°,即EB=ED,即可得证.
解答 证明:(1)∵四边形ABCD是矩形,
∴AB∥DC、AD∥BC,
∴∠ABD=∠CDB,
∵BE平分∠ABD、DF平分∠BDC,
∴∠EBD=$\frac{1}{2}$∠ABD,∠FDB=$\frac{1}{2}$∠BDC,
∴∠EBD=∠FDB,
∴BE∥DF,
又∵AD∥BC,
∴四边形BEDF是平行四边形;
(2)当∠ABE=30°时,四边形BEDF是菱形,
∵BE平分∠ABD,
∴∠ABD=2∠ABE=60°,∠EBD=∠ABE=30°,
∵四边形ABCD是矩形,
∴∠A=90°,
∴∠EDB=90°-∠ABD=30°,
∴∠EDB=∠EBD=30°,
∴EB=ED,
又∵四边形BEDF是平行四边形,
∴四边形BEDF是菱形.
点评 本题主要考查矩形的性质、平行四边形、菱形,熟练掌握矩形的性质、平行四边形的判定与菱形的判定是解题的关键.


 小学教材完全解读系列答案
小学教材完全解读系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
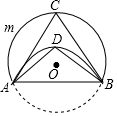 如图,将⊙O沿弦AB折叠,点C在$\widehat{AmB}$上,点D在$\widehat{AB}$上,若∠ACB=70°,则∠ADB=110°.
如图,将⊙O沿弦AB折叠,点C在$\widehat{AmB}$上,点D在$\widehat{AB}$上,若∠ACB=70°,则∠ADB=110°.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,四边形ABCD与四边形EFGH位似,位似中心点是O,$\frac{OE}{OA}$=$\frac{3}{5}$,则$\frac{FG}{BC}$=$\frac{3}{5}$.
如图,四边形ABCD与四边形EFGH位似,位似中心点是O,$\frac{OE}{OA}$=$\frac{3}{5}$,则$\frac{FG}{BC}$=$\frac{3}{5}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a≤4 | B. | a≥4 | C. | a≤-4 | D. | a≥-4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com