
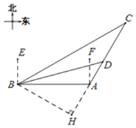
ЁОЬтФПЁПШчЭМЃЌФГЬьЮвЙњвЛЫвКЃМрДЌбВКНЕНAИлПке§ЮїЗНЕФBДІЪБЃЌЗЂЯждкBЕФББЦЋЖЋ60ЁуЗНЯђЃЌЯрОр150КЃРяДІЕФCЕугавЛПЩвЩДЌжЛе§биCAЗНЯђааЪЛЃЌCЕудкAИлПкЕФББЦЋЖЋ30ЁуЗНЯђЩЯЃЌКЃМрДЌЯђAИлПкЗЂГіжИСюЃЌжДЗЈДЌСЂМДДгAИлПкбиACЗНЯђЪЛГіЃЌдкDДІГЩЙІРЙНиПЩвЩДЌжЛЃЌДЫЪБDЕугыBЕуЕФОрРыЮЊ![]() КЃРяЃЎ
КЃРяЃЎ
ЃЈ1ЃЉЧѓBЕуЕНжБЯпCAЕФОрРыЃЛ
ЃЈ2ЃЉжДЗЈДЌДгAЕНDКНааСЫЖрЩйКЃРяЃП

ЁОД№АИЁПЃЈ1ЃЉ![]() ЕуЕНжБЯп
ЕуЕНжБЯп![]() ЕФОрРыЪЧ75КЃРяЃЛЃЈ2ЃЉжДЗЈДЌДг
ЕФОрРыЪЧ75КЃРяЃЛЃЈ2ЃЉжДЗЈДЌДг![]() ЕН
ЕН![]() КНааСЫ
КНааСЫ![]() КЃРяЃЎ
КЃРяЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнЗНЮЛНЧЕФЖЈвхЯШЧѓГіЁЯCBAКЭЁЯBCAЕФЖШЪ§ЃЌдйИљОнBH=BCЁСsinЁЯBCAМЦЫуМДПЩЕУГіД№АИЃЛ
ЃЈ2ЃЉбгГЄCAЃЌзїBHЁЭCAЕФбгГЄЯпгкЕуHЃЌИљОнЙДЙЩЖЈРэЧѓГіDHЕФжЕЃЌдйРћгУtanЁЯBAHЕФжЕМДПЩЧѓГіAHЕФжЕЃЌМДПЩЕУГіД№АИЃЎ
НтЃКЃЈ1ЃЉ![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
![]() ЃЈКЃРяЃЉЃЌ
ЃЈКЃРяЃЉЃЌ
Д№ЃК![]() ЕуЕНжБЯп
ЕуЕНжБЯп![]() ЕФОрРыЪЧ75КЃРяЃЛ
ЕФОрРыЪЧ75КЃРяЃЛ
ЃЈ2ЃЉбгГЄCAЃЌзїBHЁЭCAЕФбгГЄЯпгкЕуH
![]() КЃРяЃЌ
КЃРяЃЌ![]() КЃРяЃЌ
КЃРяЃЌ
![]() ЃЈКЃРяЃЉЃЌ
ЃЈКЃРяЃЉЃЌ
![]() ЃЌ
ЃЌ
дк![]() жаЃЌ
жаЃЌ![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
ЁрAD=DH-AH=75-25![]() ЃЈКЃРяЃЉ.
ЃЈКЃРяЃЉ.
Д№ЃКжДЗЈДЌДг![]() ЕН
ЕН![]() КНааСЫ
КНааСЫ![]() КЃРяЃЎ
КЃРяЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
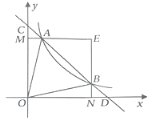
ЁОЬтФПЁПШчЭМЃЌвЛДЮКЏЪ§![]() ЕФЭМЯѓгыЗДБШР§КЏЪ§
ЕФЭМЯѓгыЗДБШР§КЏЪ§![]() ЃЈ
ЃЈ![]() ЮЊГЃЪ§ЃЌЧв
ЮЊГЃЪ§ЃЌЧв![]() ЃЉЕФЭМЯѓНЛгк
ЃЉЕФЭМЯѓНЛгк![]() ЃЌ
ЃЌ![]() СНЕуЃЌгы
СНЕуЃЌгы![]() жсКЭ
жсКЭ![]() жсЗжБ№НЛгк
жсЗжБ№НЛгк![]() СНЕуЃЌ
СНЕуЃЌ![]() жсЃЌ
жсЃЌ![]() жсЃЌДЙзуЗжБ№ЮЊ
жсЃЌДЙзуЗжБ№ЮЊ![]() ЕуЃЌЧв
ЕуЃЌЧв![]() гы
гы![]() НЛгкЕу
НЛгкЕу![]() .
.
ЃЈ1ЃЉЧѓЗДБШР§КЏЪ§ЕФБэДяЪНМАЕу![]() ЕФзјБъЃЛ
ЕФзјБъЃЛ
ЃЈ2ЃЉжБНгаДГіЗДБШР§КЏЪ§ЭМЯёЮЛгкЕквЛЯѓЯоЧв![]() ЪБздБфСП
ЪБздБфСП![]() ЕФШЁжЕЗЖЮЇЃЛ
ЕФШЁжЕЗЖЮЇЃЛ
ЃЈ3ЃЉЧѓ![]() гы
гы![]() УцЛ§ЕФБШ.
УцЛ§ЕФБШ.
![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
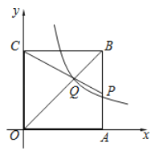
ЁОЬтФПЁПШчЭМЃЌе§ЗНаЮЕФБпГЄЮЊ![]() ЗжБ№ЮЛгк
ЗжБ№ЮЛгк![]() жсЃЌ
жсЃЌ![]() жсЩЯЃЌЕу
жсЩЯЃЌЕу![]() дк
дк![]() ЩЯЃЌ
ЩЯЃЌ![]() НЛ
НЛ![]() гкЕу
гкЕу![]() ЃЌКЏЪ§
ЃЌКЏЪ§![]() ЕФЭМЯёОЙ§Еу
ЕФЭМЯёОЙ§Еу![]() ЃЌШє
ЃЌШє![]() ЃЌдђ
ЃЌдђ![]() ЕФжЕЮЊЃЈ ЃЉ
ЕФжЕЮЊЃЈ ЃЉ
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌКЏЪ§ y kx гы y  ЕФЭМЯѓНЛгк AЁЂB СНЕуЃЌЙ§ A зї y жсЕФДЙЯпЃЌНЛКЏЪ§
ЕФЭМЯѓНЛгк AЁЂB СНЕуЃЌЙ§ A зї y жсЕФДЙЯпЃЌНЛКЏЪ§ ЕФЭМЯѓгкЕу CЃЌСЌНг BCЃЌдђЁїABC ЕФУцЛ§ЮЊЃЈ ЃЉ
ЕФЭМЯѓгкЕу CЃЌСЌНг BCЃЌдђЁїABC ЕФУцЛ§ЮЊЃЈ ЃЉ

A. 2 B. 4 C. 6 D. 8
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮвУЧжЊЕРЃЌШЮвтвЛИіе§ећЪ§nЖМПЩвдНјааетбљЕФЗжНтЃКn=pЁСqЃЈpЃЌqЪЧе§ећЪ§ЃЌЧвpЁмqЃЉЃЌдкnЕФЫљгаетжжЗжНтжаЃЌШчЙћpЃЌqСНвђЪ§жЎВюЕФОјЖджЕзюаЁЃЌЮвУЧОЭГЦpЁСqЪЧnЕФзюМбЗжНтЃЌВЂЙцЖЈЃКFЃЈnЃЉ=![]() ЃЎР§ШчЃК12ПЩвдЗжНтГЩ1ЁС12ЃЌ2ЁС6Лђ3ЁС4ЃЌвђЮЊ12Љ1ЃО6Љ2ЃО4Љ3ЃЌЫљвд3ЁС4ЪЧ12ЕФзюМбЗжНтЃЌЫљвдFЃЈ12ЃЉ=
ЃЎР§ШчЃК12ПЩвдЗжНтГЩ1ЁС12ЃЌ2ЁС6Лђ3ЁС4ЃЌвђЮЊ12Љ1ЃО6Љ2ЃО4Љ3ЃЌЫљвд3ЁС4ЪЧ12ЕФзюМбЗжНтЃЌЫљвдFЃЈ12ЃЉ=![]() ЃЎШчЙћвЛИіСНЮЛе§ећЪ§tЃЌt=10x+yЃЈ1ЁмxЁмyЁм9ЃЌxЃЌyЮЊздШЛЪ§ЃЉЃЌНЛЛЛЦфИіЮЛЩЯЕФЪ§гыЪЎЮЛЩЯЕФЪ§ЕУЕНЕФаТЪ§МѕШЅдРДЕФСНЮЛе§ећЪ§ЫљЕУЕФВюЮЊ36ЃЌФЧУДЮвУЧГЦетИіЪ§tЮЊЁАМЊЯщЪ§ЁБЃЎИљОнвдЩЯаТЖЈвхЃЌЯТСаЫЕЗЈе§ШЗЕФгаЃКЃЈ1ЃЉFЃЈ48ЃЉ=
ЃЎШчЙћвЛИіСНЮЛе§ећЪ§tЃЌt=10x+yЃЈ1ЁмxЁмyЁм9ЃЌxЃЌyЮЊздШЛЪ§ЃЉЃЌНЛЛЛЦфИіЮЛЩЯЕФЪ§гыЪЎЮЛЩЯЕФЪ§ЕУЕНЕФаТЪ§МѕШЅдРДЕФСНЮЛе§ећЪ§ЫљЕУЕФВюЮЊ36ЃЌФЧУДЮвУЧГЦетИіЪ§tЮЊЁАМЊЯщЪ§ЁБЃЎИљОнвдЩЯаТЖЈвхЃЌЯТСаЫЕЗЈе§ШЗЕФгаЃКЃЈ1ЃЉFЃЈ48ЃЉ=![]() ЃЛЃЈ2ЃЉШчЙћвЛИіе§ећЪ§mЪЧСэЭтвЛИіе§ећЪ§nЕФЦНЗНЃЌЮвУЧГЦе§ећЪ§mЪЧЭъШЋЦНЗНЪ§ЃЌдђЖдШЮвтвЛИіЭъШЋЦНЗНЪ§mЃЌзмгаFЃЈmЃЉ=1ЃЛЃЈ3ЃЉ15КЭ26ЪЧЁАМЊЯщЪ§ЁБЃЛЃЈ4ЃЉЁАМЊЯщЪ§ЁБжаЃЌFЃЈtЃЉЕФзюДѓжЕЮЊ
ЃЛЃЈ2ЃЉШчЙћвЛИіе§ећЪ§mЪЧСэЭтвЛИіе§ећЪ§nЕФЦНЗНЃЌЮвУЧГЦе§ећЪ§mЪЧЭъШЋЦНЗНЪ§ЃЌдђЖдШЮвтвЛИіЭъШЋЦНЗНЪ§mЃЌзмгаFЃЈmЃЉ=1ЃЛЃЈ3ЃЉ15КЭ26ЪЧЁАМЊЯщЪ§ЁБЃЛЃЈ4ЃЉЁАМЊЯщЪ§ЁБжаЃЌFЃЈtЃЉЕФзюДѓжЕЮЊ![]() ЃЎ ( )
ЃЎ ( )
A.1ИіB.2ИіC.3ИіD.4Иі
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПМЧФГЩЬЦЗЯњЪлЕЅМлЮЊxдЊЃЌЩЬМвЯњЪлДЫжжЩЬЦЗУПдТЛёЕУЕФЯњЪлРћШѓЮЊyдЊЃЌЧвyЪЧЙигкxЕФЖўДЮКЏЪ§ЃЎвбжЊЕБЩЬМвНЋДЫжжЩЬЦЗЯњЪлЕЅМлЗжБ№ЖЈЮЊ55дЊЛђ75дЊЪБЃЌЫћУПдТОљПЩЛёЕУЯњЪлРћШѓ1800дЊЃЛЕБЩЬМвНЋДЫжжЩЬЦЗЯњЪлЕЅМлЖЈЮЊ80дЊЪБЃЌЫћУПдТПЩЛёЕУЯњЪлРћШѓ1550дЊЃЌдђyгыxЕФКЏЪ§ЙиЯЕЪНЪЧЃЈ ЃЉ
A.yЃНЉЃЈxЉ60ЃЉ2+1825B.yЃНЉ2ЃЈxЉ60ЃЉ2+1850
C.yЃНЉЃЈxЉ65ЃЉ2+1900D.yЃНЉ2ЃЈxЉ65ЃЉ2+2000
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
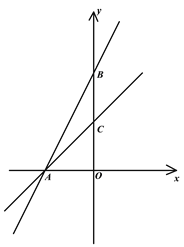
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌжБЯпAB![]() гыxжсЃЌyжсЃЌНЛгкAЁЂBСНЕуЃЌЕуCЪЧBOЕФжаЕуЧв
гыxжсЃЌyжсЃЌНЛгкAЁЂBСНЕуЃЌЕуCЪЧBOЕФжаЕуЧв![]()
ЃЈ1ЃЉЧѓжБЯпACЕФНтЮіЪНЃЛ
ЃЈ2ЃЉШєЕуMЪЧжБЯпACЕФвЛЕуЃЌЕБ![]() ЪБЃЌЧѓЕуMЕФзјБъ.
ЪБЃЌЧѓЕуMЕФзјБъ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
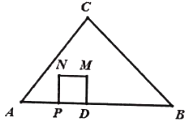
ЁОЬтФПЁПдк![]() жаЃЌ
жаЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌЕуDдкБпABЩЯЃЌЧв
ЃЌЕуDдкБпABЩЯЃЌЧв![]() ЃЌЖЏЕуPДгЕуAГіЗЂЃЌвдУПУы1ИіЕЅЮЛГЄЖШЕФЫйЖШЯђжеЕуBдЫЖЏЃЌвдPDЮЊБпЯђЩЯзіе§ЗНаЮ
ЃЌЖЏЕуPДгЕуAГіЗЂЃЌвдУПУы1ИіЕЅЮЛГЄЖШЕФЫйЖШЯђжеЕуBдЫЖЏЃЌвдPDЮЊБпЯђЩЯзіе§ЗНаЮ![]() ЃЌЩшЕуPдЫЖЏЕФЪБМфЮЊ
ЃЌЩшЕуPдЫЖЏЕФЪБМфЮЊ![]() УыЃЌе§ЗНаЮ
УыЃЌе§ЗНаЮ![]() гы
гы![]() жиЕўВПЗжЕФУцЛ§ЮЊ
жиЕўВПЗжЕФУцЛ§ЮЊ![]() ЃЎ
ЃЎ
ЃЈ1ЃЉгУКЌга![]() ЕФДњЪ§ЪНБэЪОЯпЖЮ
ЕФДњЪ§ЪНБэЪОЯпЖЮ![]() ЕФГЄЃЎ
ЕФГЄЃЎ
ЃЈ2ЃЉЕБЕу![]() Тфдк
Тфдк![]() ЕФБпЩЯЪБЃЌЧѓ
ЕФБпЩЯЪБЃЌЧѓ![]() ЕФжЕЃЎ
ЕФжЕЃЎ
ЃЈ3ЃЉЧѓ![]() гы
гы![]() ЕФКЏЪ§ЙиЯЕЪНЃЎ
ЕФКЏЪ§ЙиЯЕЪНЃЎ
ЃЈ4ЃЉЕБЕуPдкЯпЖЮADЩЯдЫЖЏЪБЃЌзіЕуNЙигкCDЕФЖдГЦЕу![]() ЃЌЕБ
ЃЌЕБ![]() гы
гы![]() ЕФФГвЛИіЖЅЕуЕФСЌЯпЦНЗж
ЕФФГвЛИіЖЅЕуЕФСЌЯпЦНЗж![]() ЕФУцЛ§ЪБЃЌЧѓ
ЕФУцЛ§ЪБЃЌЧѓ![]() ЕФжЕЃЎ
ЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
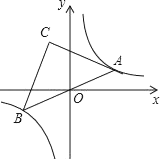
ЁОЬтФПЁПШчЭМЃЌЕуAЪЧЫЋЧњЯпy=![]() дкЕквЛЯѓЯоЩЯЕФвЛЖЏЕуЃЌСЌНгAOВЂбгГЄНЛСэвЛЗжжЇгкЕуBЃЌвдABЮЊаББпзїЕШбќRtЁїABCЃЌЕуCдкЕкЖўЯѓЯоЃЌЫцзХЕуAЕФдЫЖЏЃЌЕуCЕФЮЛжУвВВЛЖЯЕФБфЛЏЃЌЕЋЪМжедквЛКЏЪ§ЭМЯѓЩЯдЫЖЏЃЌдђетИіКЏЪ§ЕФНтЮіЪНЮЊ_____ЃЎ
дкЕквЛЯѓЯоЩЯЕФвЛЖЏЕуЃЌСЌНгAOВЂбгГЄНЛСэвЛЗжжЇгкЕуBЃЌвдABЮЊаББпзїЕШбќRtЁїABCЃЌЕуCдкЕкЖўЯѓЯоЃЌЫцзХЕуAЕФдЫЖЏЃЌЕуCЕФЮЛжУвВВЛЖЯЕФБфЛЏЃЌЕЋЪМжедквЛКЏЪ§ЭМЯѓЩЯдЫЖЏЃЌдђетИіКЏЪ§ЕФНтЮіЪНЮЊ_____ЃЎ
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com