
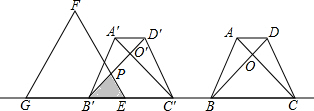
分析 (1)先根据梯形的面积公式求出梯形的高,然后作出等腰梯形的两条高AM,DN,易得△ABM≌△DCN,四边形AMND是矩形,进而可得BM=MN=NC=2,然后利用勾股定理即可求出等腰梯形ABCD的对角线长;
(2)过点P作PH⊥B′E,垂足为H,过点F作FQ⊥GE,垂足为Q,由题意可得:BB′=8,由BE=5,进而可得:B′E=3,由(1)知:△BDN是等腰直角三角形,进而可得∠DBN=45°,即∠PB′H=45°,从而可得:△PB′H是等腰直角三角形,由△EFG是边长为a的等边三角形,可得:∠FEG=60°,进而可得∠EPH=30°,然后设HE=x,然后用含x的式子表示B′E=($\sqrt{3}$+1)x,然后由B′E=3,进而可求x的值,进而可求出△B′PE的面积,然后根据S△B′PE是等边三角形EFG的$\frac{\sqrt{3}-1}{2}$,即可求出等边三角形边长a.
解答 解:(1)作AM⊥BC,DN⊥BC,垂足为分别为M、N,
可得:∠AMB=∠DNC=90°、AM=DN、四边形AMND是矩形,
∴MN=AD=2,
∵梯形ABCD是等腰梯形,
∴AB=DC,∠ABC=∠DCB,AC=BD,
在Rt△ABM和Rt△DCN中,
∵$\left\{\begin{array}{l}{AB=DC}\\{AM=DN}\end{array}\right.$,
∴Rt△ABM≌Rt△DCN(HL)
∴BM=CN,
∵BM+CN=BC-MN=4,
∴BM=CN=2,
∴BN=MC=4,
∵S梯形ABCD=$\frac{1}{2}$(AD+BC)•AM,
∴$\frac{1}{2}×$(2+6)×AM=16,
解得:AM=4,
∴DN=AM=4,
在Rt△AMC中,由勾股定理得:
AC=$\sqrt{A{M}^{2}+M{C}^{2}}$=4$\sqrt{2}$,
∴AC=BD=4$\sqrt{2}$;
(2)过点P作PH⊥B′E,垂足为H,过点F作FQ⊥GE,垂足为Q,
由题意可得:BB′=8,
∵BE=5,
∴B′E=BB′-BE=3,
由(1)知:△BDN是等腰直角三角形,
∴∠DBN=45°,即∠PB′H=45°,
∴△PB′H是等腰直角三角形,
∴PH=B′H,
∴△EFG是边长为a的等边三角形,
∴∠FEG=60°,GQ=QE=$\frac{1}{2}$QE=$\frac{1}{2}$a,
∴∠EPH=30°,
设HE=x,则PE=2x,
由勾股定理得:PH=$\sqrt{3}$x,
∴B′H=$\sqrt{3}x$,
∴B′E=($\sqrt{3}$+1)x,
∵B′E=3,
∴($\sqrt{3}$+1)x=3,
解得:x=$\frac{3(\sqrt{3}-1)}{2}$,
∴PH=$\sqrt{3}$x=$\frac{9-3\sqrt{3}}{2}$
∴S${\;}_{△{B}^{′}PE}$=$\frac{1}{2}$•B′E•PH=$\frac{1}{2}$×3×$\frac{9-3\sqrt{3}}{2}$=$\frac{27-9\sqrt{3}}{4}$,
在Rt△FGQ中,由勾股定理得:
FQ=$\frac{\sqrt{3}a}{2}$,
S△FGE=$\frac{1}{2}•$GE•FQ=$\frac{\sqrt{3}}{4}{a}^{2}$,
∵S△B′PE是等边三角形EFG的$\frac{\sqrt{3}-1}{2}$,
∴$\frac{27-9\sqrt{3}}{4}$=$\frac{\sqrt{3}-1}{2}$•$\frac{\sqrt{3}}{4}{a}^{2}$,
解得a=±3$\sqrt{2}$,
∵a不能为负数,
∴a=3$\sqrt{2}$.
点评 此题是四边形的综合题,主要考查了等腰梯形的有关性质,等边三角形的性质等知识,解题的关键是:添加适当的辅助线,判断△BDN是等腰直角三角形,△PB′H是等腰直角三角形.


 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
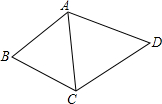 如图,四边形ABCD中,BA=BC,DA=DC,且sin∠D=$\frac{3}{5}$,∠B=45°,则$\frac{{S}_{△ABC}}{{S}_{△ADC}}$=$\frac{\sqrt{2}+1}{3}$.
如图,四边形ABCD中,BA=BC,DA=DC,且sin∠D=$\frac{3}{5}$,∠B=45°,则$\frac{{S}_{△ABC}}{{S}_{△ADC}}$=$\frac{\sqrt{2}+1}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com