
【题目】如图,把△ABC经过一定的变换得到△A′B′C′,如果△ABC边上点P的坐标为(a,b),那么这个点在△A′B′C′中的对应点P′的坐标为( )
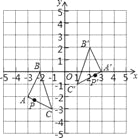
A. (﹣a,b﹣2) B. (﹣a,b+2) C. (﹣a+2,﹣b) D. (﹣a+2,b+2)
 黄冈创优卷系列答案
黄冈创优卷系列答案科目:初中数学 来源: 题型:
【题目】如图,在四边形![]() 中,已知
中,已知![]() ,
,![]() ,且
,且![]() .
.

(1)填空:![]() _____,
_____,![]() ______,
______,![]() _______;
_______;
(2)点![]() 为射线
为射线![]() 上一任意一点,连接
上一任意一点,连接![]() ,作
,作![]() 的平分线
的平分线![]() ,交射线
,交射线![]() 于点
于点![]() ,作
,作![]() 的平分线
的平分线![]() ,交直线
,交直线![]() 于点
于点![]() ,请探究射线
,请探究射线![]() 与
与![]() 之间的位置关系,并加以证明;
之间的位置关系,并加以证明;
(3)连接![]() ,若
,若![]() 恰好平分
恰好平分![]() ,则在(2)问的条件下,是否存在角度
,则在(2)问的条件下,是否存在角度![]() ,使得当
,使得当![]() 时,有
时,有![]() (其中
(其中![]() 为不超过10的正整数)?若存在,求出
为不超过10的正整数)?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲乙两件服装的进价共500元,商场决定将甲服装按30%的利润定价,乙服装按20%的利润定价,实际出售时,两件服装均按9折出售,商场卖出这两件服装共获利67元.
(1)求甲乙两件服装的进价各是多少元;
(2)由于乙服装畅销,制衣厂经过两次上调价格后,使乙服装每件的进价达到242元,求每件乙服装进价的平均增长率;
(3)若每件乙服装进价按平均增长率再次上调,商场仍按9折出售,定价至少为多少元时,乙服装才可获得利润(定价取整数).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在四个完全相同的小球上分别写上1,2,3,4四个数字,然后装入一个不透明的口袋内搅匀,从口袋内取出一个球记下数字后作为点P的横坐标x,放回袋中搅匀,然后再从袋中取出一个球记下数字后作为点P的纵坐标y,则点P(x,y)落在直线y=﹣x+5上的概率是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】结合“爱市西,爱生活,会创新”的主题,某同学设计了一款“地面霓虹探测灯”,增加美观的同时也为行人的夜间行路带去了方便.他的构想如下:在平面内,如图1所示,灯![]() 射线从
射线从![]() 开始顺时针旋转至
开始顺时针旋转至![]() 便立即回转,灯
便立即回转,灯![]() 射线从
射线从![]() 开始顺时针旋转至
开始顺时针旋转至![]() 便立即回转,两灯不停交叉照射巡视.若灯
便立即回转,两灯不停交叉照射巡视.若灯![]() 转动的速度是每秒2度,灯
转动的速度是每秒2度,灯![]() 转动的速度是每秒1度.假定主道路是平行的,即
转动的速度是每秒1度.假定主道路是平行的,即![]() ,且
,且![]() .
.
(1)填空:![]() ______
______![]() ;
;
(2)若灯![]() 射线先转动60秒,灯
射线先转动60秒,灯![]() 射线才开始转动,在灯
射线才开始转动,在灯![]() 射线到达
射线到达![]() 之前,
之前,![]() 灯转动几秒,两灯的光束互相平行?
灯转动几秒,两灯的光束互相平行?
(3)如图2,若两灯同时转动,在灯![]() 射线到达
射线到达![]() 之前,若射出的光束交于点
之前,若射出的光束交于点![]() ,过
,过![]() 作
作![]() 交
交![]() 于点
于点![]() ,且
,且![]() ,则在转动过程中,请探究
,则在转动过程中,请探究![]() 与
与![]() 的数量关系是否发生变化?若不变,请求出其数量关系;若改变,请说明理由.
的数量关系是否发生变化?若不变,请求出其数量关系;若改变,请说明理由.
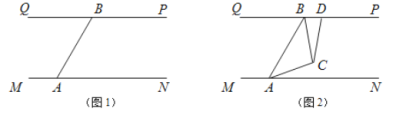
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了更好治理西太湖水质,保护环境,市治污公司决定购买10 台污水处理设备,现有A、B两种型号的设备,其中每台的价格,月处理污水量如下表:

经调查:购买-台A型设备比购买一-台B型设备多2万元,购买2台A型设备比购买4台B型设备少4万元.
(1)求a、b的值;
(2)经预算:市治污公司购买污水处理设备的资金不超过47万元,并且该月要求处理西太湖的污水量不低于1860 吨,则有哪几种购买方案?请指出最省钱的一种购买方案,并指出相应的费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,O为直线AB上一点,过点O作射线OC,![]() ,将一直角三角板
,将一直角三角板![]() 的直角顶点放在点O处,一边ON在射线OA上,另一边OM与OC都在直线AB的上方.
的直角顶点放在点O处,一边ON在射线OA上,另一边OM与OC都在直线AB的上方.
![]() 将图1中的三角板绕点O以每秒
将图1中的三角板绕点O以每秒![]() 的速度沿逆时针方向旋转一周
的速度沿逆时针方向旋转一周![]() 如图2,经过t秒后,ON落在OC边上,则
如图2,经过t秒后,ON落在OC边上,则![]() ______秒
______秒![]() 直接写结果
直接写结果![]() .
.
![]() 如图2,三角板继续绕点O以每秒
如图2,三角板继续绕点O以每秒![]() 的速度沿逆时针方向旋转到起点OA上
的速度沿逆时针方向旋转到起点OA上![]() 同时射线OC也绕O点以每秒
同时射线OC也绕O点以每秒![]() 的速度沿逆时针方向旋转一周,
的速度沿逆时针方向旋转一周,
![]() 当OC转动9秒时,求
当OC转动9秒时,求![]() 的度数.
的度数.
![]() 运动多少秒时,
运动多少秒时,![]() ?请说明理由.
?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,甲乙两人在游泳池A处发现游泳池中的P处有人求救,甲立即跳入池中去救人,速度为1米/秒,乙以3.5米/秒的速度沿游泳池边跑到距A不远处的B处,捡起一个游泳圈再跳入池中去救人,甲游了20秒到达P处,两秒后乙到达P处.若∠PAB与∠PBC互余,且cos∠PBC= ![]() ,求乙的游泳速度.
,求乙的游泳速度. 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com