(1)解:作图如图.
证明:在△ABO与△ADO中,
∵

,
∴△ABO≌△ADO(SAS),
∴BO=OD,
∵AD∥BC,
∴∠OBE=∠ODA,∠OAD=∠OEB,
在△BOE与△DOA中,
∵

,
∴△BOE≌△DOA(AAS),
∴BE=AD(平行且相等),
∴四边形ABED为平行四边形,另AB=AD,

∴四边形ABED为菱形;
(2)证明:设DE=2a,则CE=4a,过点D作DF⊥BC,
∵∠ABC=60°,∴∠DEF=60°,
∴∠EDF=30°,∴EF=

DE=a,
则DF=

,CF=CE-EF=4a-a=3a,
∴

,
∴DE=2a,EC=4a,CD=
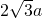
,构成一组勾股数,
∴△EDC为直角三角形,则ED⊥DC.
分析:(1)分别以点B、D为圆心,以大于AB的长度为半径,分别作弧,且两弧交于一点P,连接AP,则AP即为∠BAD的平分线,且AP交BC于点E;
可通过证△BOE≌△BOA,得AO=OE,则AD与BE平行且相等,由此证得四边形ABED是平行四边形,而AB=AD,根据一组邻边相等的平行四边形是菱形,即可证得所求的结论;
(2)已知了EC、BE的比例关系,可用未知数表示出BE、EC的长;过D作DF⊥BC于F,在Rt△DEF中,易知∠DEF=∠ABC=60°,可用DE(即BE)的长表示出EF、DF,进而表示出FC的长;在Rt△CFD中,根据DF、CF的长,可由勾股定理求出CD的长,进而可根据DE、EC、CD的长由勾股定理证得DE⊥DC.
点评:此题主要考查了梯形的性质、尺规作图-角平分线的作法、菱形的判定和性质、勾股定理的应用等知识.

 写作法),并证明四边形ABED是菱形;
写作法),并证明四边形ABED是菱形; ,
, ,
,
 DE=a,
DE=a, ,CF=CE-EF=4a-a=3a,
,CF=CE-EF=4a-a=3a, ,
,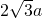 ,构成一组勾股数,
,构成一组勾股数,

 如图,已知梯形ABCD中,AD∥CB,E,F分别是BD,AC的中点,BD平分∠ABC.
如图,已知梯形ABCD中,AD∥CB,E,F分别是BD,AC的中点,BD平分∠ABC.