Question

10．如图，在梯形ABCD中，AD∥BC，∠B=90°，BC=6，AD=3，∠DCB=30°．点E、F同时从B点出发，沿射线BC向右匀速移动，已知F点移动速度是E点移动速度的2倍，以EF为一边在CB的上方作等边△EFG，设E点移动距离为x（x＞0）．
（1）△EFG的边长是x（用含有x的代数式表示），当x=2时，点G的位置在D；
（2）若△EFG与梯形ABCD重叠部分面积是y，求y与x之间的函数关系式；
（3）探究（2）中得到的函数y在x取何值时，存在最大值？并求出最大值．

Answer 1

分析 （1）根据等边三角形的三边相等，则△EFG的边长是点E移动的距离；根据等边三角形的三线合一和F点移动速度是E点移动速度的2倍，即可分析出BF=4，此时等边三角形的边长是2，则点G和点D重合；
（2）①当0＜x≤2时，重叠部分的面积即为等边三角形的面积；
②当2＜x≤6时，分两种情况：当2＜x＜3时和当3≤x≤6时及x＞6，进行计算；
（3）分别求得（2）中每一种情况的最大值，再进一步比较取其中的最大值即可．

解答 解：（1）∵点E、F同时从B点出发，沿射线BC向右匀速移动，且F点移动速度是E点移动速度的2倍，
∴BF=2BE=2x，
∴EF=BF-BE=2x-x=x，
∴△EFG的边长是x；
过D作DH⊥BC于H，得矩形ABHD及直角△CDH，连接DE、DF．
在直角△CDH中，∵∠C=30°，CH=BC-AD=3，
∴DH=CH•tan30°=3×$\frac{\sqrt{3}}{3}$当x=2时，BE=EF=2，
∵△EFG是等边三角形，且DH⊥BC交点H，
∴EH=HF=1
∴DE=DF=$\sqrt{D{H}^{2}+E{H}^{2}}$=2，
∴△DEF是等边三角形，
∴点G的位置在D点．
故答案为x，D点；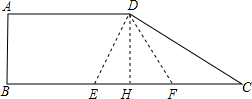

（2）①当0＜x≤2时，△EFG在梯形ABCD内部，所以y=$\frac{\sqrt{3}}{4}$x²；
②分两种情况：
Ⅰ．当2＜x＜3时，如图1，点E、点F在线段BC上，
△EFG与梯形ABCD重叠部分为四边形EFNM，
∵∠FNC=∠FCN=30°，∴FN=FC=6-2x．∴GN=3x-6．
∵在Rt△NMG中，∠G=60°，GN=3x-6，
∴GM=$\frac{1}{2}$（3x-6），
由勾股定理得：MN=$\frac{\sqrt{3}}{2}$（3x-6），
∴S_△GMN=$\frac{1}{2}$×GM×MN=$\frac{1}{2}$×$\frac{1}{2}$（3x-6）×$\frac{\sqrt{3}}{2}$（3x-6）=$\frac{\sqrt{3}}{8}$（3x-6）²，
所以，此时y=$\frac{\sqrt{3}}{4}$x²-$\frac{\sqrt{3}}{8}$（3x-6）²=-$\frac{7\sqrt{3}}{8}{x}^{2}+\frac{9\sqrt{3}}{2}x-\frac{9\sqrt{3}}{2}$；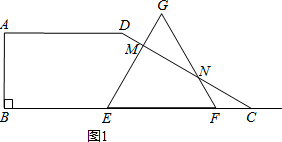

Ⅱ．当3≤x≤6时，如图2，点E在线段BC上，点F在射线CH上，
△EFG与梯形ABCD重叠部分为△ECP，
∵EC=6-x，
∴y=$\frac{\sqrt{3}}{8}$（6-x）²=$\frac{\sqrt{3}}{8}$x²-$\frac{3\sqrt{3}}{2}$x+$\frac{9\sqrt{3}}{2}$，
Ⅲ．当x＞6时，点E，F都在线段BC的延长线上，没公共部分，
∴y=0；
（3）当0＜x≤2时，
∵y=$\frac{\sqrt{3}}{4}$x²，在x＞0时，y随x增大而增大，
∴x=2时，y_最大=$\sqrt{3}$；
当2＜x＜3时，∵y=-$\frac{7\sqrt{3}}{8}{x}^{2}+\frac{9\sqrt{3}}{2}x-\frac{9\sqrt{3}}{2}$在x=$\frac{18}{7}$时，y_最大=$\frac{9\sqrt{3}}{7}$；
当3≤x≤6时，∵y=$\frac{\sqrt{3}}{8}x-\frac{3\sqrt{3}}{2}x+\frac{9\sqrt{3}}{2}$，在x＜6时，y随x增大而减小，
∴x=3时，y_最大=$\frac{9\sqrt{3}}{8}$．
综上所述：当x=$\frac{18}{7}$时，y_最大=$\frac{9\sqrt{3}}{7}$．

点评 此题是四边形综合题，主要考查了梯形的性质，等边三角形的性质和判定，勾股定理，图形的面积，解本题的关键是画出图形，是一道动态题，难度较大，注意不同的情况，能够熟练求得二次函数的最值．