
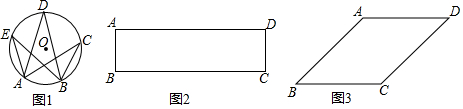
分析 (1)①直接利用圆的性质得出BC的中点,进而得出⊙O,即可得出P点位置;
②利用①中所求,进而利用AB<$\frac{1}{2}$BC时,AB=$\frac{1}{2}$BC时,AB>$\frac{1}{2}$BC时,分别得出答案;
(2)利用圆周角定理结合圆的相关性质得出符合题意的图形.
解答  解:(1)①如图2所示:
解:(1)①如图2所示:
作法:以BC为直径作⊙O,交AD于P1、P2
P1、P2 为所求作的点P,
②AB<$\frac{1}{2}$BC时,点P有两个;
AB=$\frac{1}{2}$BC时,点P有且只有1个;
AB>$\frac{1}{2}$BC时,点P有0个;
(2)如图3所示:
连接AC,作△ADC的外接圆⊙O,再以C为圆心,CD的长为半径画弧,与⊙O相交于点E,则四边形ABCE即为所求反例图形.
点评 此题主要考查了圆的综合以及平行四边形的性质等知识,正确应用圆周角定理是解题关键.


科目:初中数学 来源: 题型:选择题
| A. | -10 | B. | 10 | C. | 12 | D. | -12 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
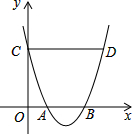 如图,抛物线y=ax2+bx+c与x轴交于点A、B,与y轴交于点C,过点C作CD∥x轴,与抛物线交于点D,若OA=1,CD=4,则线段AB的长为( )
如图,抛物线y=ax2+bx+c与x轴交于点A、B,与y轴交于点C,过点C作CD∥x轴,与抛物线交于点D,若OA=1,CD=4,则线段AB的长为( )| A. | 2 | B. | 1 | C. | 3 | D. | 1.5 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (-4,-3) | B. | (4,-3) | C. | (-3,-4) | D. | (3,-4) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
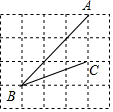 如图,在网格中,小正方形的边长均为1,点A,B,C都在格点上,则∠ABC的正切值是( )
如图,在网格中,小正方形的边长均为1,点A,B,C都在格点上,则∠ABC的正切值是( )| A. | 2 | B. | $\frac{1}{2}$ | C. | $\frac{\sqrt{5}}{5}$ | D. | $\frac{2\sqrt{5}}{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | m2-(2m-n-p)=m2-2m+n+p | B. | m-n+p-q=m-(n+q-p) | ||
| C. | 3m-5n-1+2p=-(-3m)-[5n-(2p-1)] | D. | m+1-(-n+p)=-(-1+n-m+p) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com