
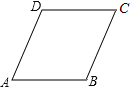
【题目】如图,凸四边形ABCD中,AB∥CD,且AB+BC=CD+AD.求证:ABCD是平行四边形。
【答案】详见解析.
证明:假设ABCD不是平行四边形,即AB≠CD,
不妨设AB>CD.在AB边上取点E,使AE=CD,则AECD是平行四边形,
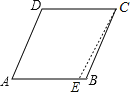
∴AD=CE,
由AB+BC=CD+AD,
即(AE+EB)+BC=CD+AD,
∴EB+BC=CE,与三角形不等式EB+BC>CE矛盾,
因此,ABCD必是平行四边形。
【解析】试题分析:
利用已知条件不能直接证明四边形ABCD是平行四边形,故考虑用反证法,假设四边形ABCD不是平行四边形,则可设AB>CD,所以在AB上取点E,使AE=CD,然后经过推理得出矛盾,从而假设不成立,故原命题成立.
试题解析:
证明:假设ABCD不是平行四边形,即AB≠CD,
不妨设AB>CD.在AB边上取点E,使AE=CD,则AECD是平行四边形,

∴AD=CE,
由AB+BC=CD+AD,
即(AE+EB)+BC=CD+AD,
∴EB+BC=CE,与三角形不等式EB+BC>CE矛盾,
因此,ABCD必是平行四边形。


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点P的坐标为(0,4),直线y=x﹣3与x轴、y轴分别交于点A,B,点M是直线AB上的一个动点,则PM长的最小值为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】据中央气象台今年1月8日的预报,下列四个地区的最低气温分别是:哈尔滨-11 ℃,杭州6 ℃,兰州-5 ℃,海口27 ℃,则其中气温最高的地区是____,气温最低的地区是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC和△ADE都是等边三角形,点D在BC边上,AB边上有一点F,且BF=DC,连接EF、EB。
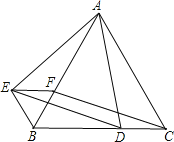
(1)求证:△ABE≌△ACD;
(2)求证:四边形EFCD是平行四边形。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市举行“行动起来,对抗雾霾”为主题的植树活动,某街道积极响应,决定对该街道进行绿化改造,共购进甲、乙两种树共500棵,已知甲树每棵800元,乙树每棵1200元.
(1)若购买两种树总金额为560000元,求甲、乙两种树各购买了多少棵?
(2)若购买甲树的金额不少于购买乙树的金额,至少应购买甲树多少棵?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司欲聘请一位员工,三位应聘者A、B、C的原始评分如下表:
应聘者 | 仪表 | 工作经验 | 电脑操作 | 社交能力 | 工作效率 |
A | 4 | 5 | 5 | 3 | 3 |
B | 4 | 3 | 3 | 5 | 4 |
C | 3 | 3 | 4 | 4 | 4 |
(1)如果按五项原始评分的平均分,应聘用谁;
(2)如果按仪表、工作经验、电脑操作、社交能力、工作效率的原始评分分别占10%,15%,20%,25%,30%综合评分,谁将被聘用?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为加强学生的文化素养,阳光书店与学校联合开展读书活动,书店购进了一定数量的名著A和B两种图书到学校进行销售,其中A的标价是45元,比B的标价多25元,A的进价是B的进价的![]() .为此,学校划拨了1800元用于购买A,划拨了800元用于购买B.
.为此,学校划拨了1800元用于购买A,划拨了800元用于购买B.
(1)阳光书店在此次销售中盈利不低于800元,则名著B的进价最多是多少元?
(2)阳光书店为支持学校的读书活动,决定将A、B两种名著的标价都下降m%后卖给学校,这样,学校购买名著A的数量不变,B还可多买2m本,且总购书款不变,求m的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com