
 如图,在△ABC中,DE∥BC,若AD=3,BD=4,BC=5,则DE的长为( )
如图,在△ABC中,DE∥BC,若AD=3,BD=4,BC=5,则DE的长为( )| A. | $\frac{15}{4}$ | B. | $\frac{15}{7}$ | C. | $\frac{12}{5}$ | D. | $\frac{5}{2}$ |
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:初中数学 来源: 题型:解答题
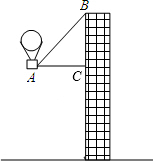 如图,有一热气球到达A处时,仪器显示其正前方一高楼顶部B的仰角是43°,与楼的水平距离AC为12米,为了安全飞越高楼,气球应至少再上升多少米?(结果精确到0.1米)
如图,有一热气球到达A处时,仪器显示其正前方一高楼顶部B的仰角是43°,与楼的水平距离AC为12米,为了安全飞越高楼,气球应至少再上升多少米?(结果精确到0.1米)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
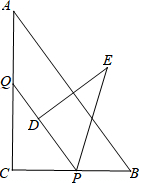 如图,Rt△ABC中,∠C=90°,AB=5,BC=3,点P、Q分别在BC、AC上,CP=3x,CQ=4x (0<x<1),把△PCQ绕点P旋转,得到△PDE,点D落在线段PQ上.
如图,Rt△ABC中,∠C=90°,AB=5,BC=3,点P、Q分别在BC、AC上,CP=3x,CQ=4x (0<x<1),把△PCQ绕点P旋转,得到△PDE,点D落在线段PQ上.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 车辆随机到达一个路口,遇到红灯 | |
| B. | 两条线断可以组成一个三角形 | |
| C. | 400人中有两个人的生日在同一天 | |
| D. | 掷一枚质地均匀的骰子,掷出的点数是质数 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com