
【题目】如图,在△ABC中,AB=AC,D、E、F分别为AB、BC、AC的中点,则下列结论:①△ADF≌△FEC;②四边形ADEF为菱形;③![]() 。其中正确的结论是____________.(填写所有正确结论的序号)
。其中正确的结论是____________.(填写所有正确结论的序号)

【答案】①②③
【解析】
①根据三角形的中位线定理可得出AD=FE、AF=FC、DF=EC,进而可证出△ADF≌△FEC(SSS),结论①正确;
②根据三角形中位线定理可得出EF∥AB、EF=AD,进而可证出四边形ADEF为平行四边形,由AB=AC结合D、F分别为AB、AC的中点可得出AD=AF,进而可得出四边形ADEF为菱形,结论②正确;
③根据三角形中位线定理可得出DF∥BC、DF=![]() BC,进而可得出△ADF∽△ABC,再利用相似三角形的性质可得出
BC,进而可得出△ADF∽△ABC,再利用相似三角形的性质可得出![]() ,结论③正确.此题得解.
,结论③正确.此题得解.
①∵D、E、F分别为AB、BC、AC的中点,
∴DE、DF、EF为△ABC的中位线,
∴AD=![]() AB=FE,AF=
AB=FE,AF=![]() AC=FC,DF=
AC=FC,DF=![]() BC=EC.
BC=EC.
在△ADF和△FEC中,
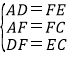 ,
,
∴△ADF≌△FEC(SSS),结论①正确;
②∵E、F分别为BC、AC的中点,
∴EF为△ABC的中位线,
∴EF∥AB,EF=![]() AB=AD,
AB=AD,
∴四边形ADEF为平行四边形.
∵AB=AC,D、F分别为AB、AC的中点,
∴AD=AF,
∴四边形ADEF为菱形,结论②正确;
③∵D、F分别为AB、AC的中点,
∴DF为△ABC的中位线,
∴DF∥BC,DF=![]() BC,
BC,
∴△ADF∽△ABC,
∴![]() ,结论③正确.
,结论③正确.
故答案为:①②③.


科目:初中数学 来源: 题型:
【题目】我们知道,一元二次方程x2=﹣1没有实数根,即不存在一个实数的平方等于﹣1,若我们规定一个新数i,使其满足i2=﹣1(即x2=﹣1方程有一个根为i),并且进一步规定:一切实数可以与新数进行四则运算,且原有的运算法则仍然成立,于是有i1=i,i2=﹣1,i3=i2i=(﹣1)i,i4=(i2)2=(﹣1)2=1,从而对任意正整数n,我们可得到i4n+1=i4ni=(i4)ni,同理可得i4n+2=﹣1,i4n+3=﹣i,i4n=1,那么,i+i2+i3+i4+…+i2016+i2017的值为( )
A. 0 B. 1 C. ﹣1 D. i
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() (
(![]() 是常数)经过点
是常数)经过点![]() .
.
(![]() )求该抛物线的解析式和顶点坐标.
)求该抛物线的解析式和顶点坐标.
(![]() )抛物线与
)抛物线与![]() 轴另一交点为点
轴另一交点为点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,平行于
,平行于![]() 轴的直线
轴的直线![]() 与抛物线交于点
与抛物线交于点![]() ,
, ![]() ,与直线
,与直线![]() 交于点
交于点![]() .
.
①求直线![]() 的解析式.
的解析式.
②若![]() ,结合函数的图像,求
,结合函数的图像,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明租用共享单车从家出发,匀速骑行到相距![]() 米的图书馆还书.小明出发的同时,他的爸爸以每分钟
米的图书馆还书.小明出发的同时,他的爸爸以每分钟![]() 米的速度从图书馆沿同一条道路步行回家,小明在图书馆停留了
米的速度从图书馆沿同一条道路步行回家,小明在图书馆停留了![]() 分钟后沿原路按原速返回.设他们出发后经过
分钟后沿原路按原速返回.设他们出发后经过![]() (分)时,小明与家之间的距离为
(分)时,小明与家之间的距离为![]() (米),小明爸爸与家之间的距离为
(米),小明爸爸与家之间的距离为![]() (米),图中折线
(米),图中折线![]() 、线段
、线段![]() 分别表示
分别表示![]() 、
、![]() 与
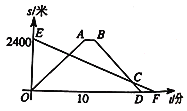
与![]() 之间的函数关系的图象.小明从家出发,经过___分钟在返回途中追上爸爸.
之间的函数关系的图象.小明从家出发,经过___分钟在返回途中追上爸爸.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠A=120°,∠B=40°,如果过点A的一条直线l把△ABC分割成两个等腰三角形,直线l与BC交于点D,那么∠ADC的度数是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在等边△ABC中,点P,Q是BC边上的两个动点(不与点B、C重合),且AP=AQ.
(1)如图1,已知,∠BAP=20°,求∠AQB的度数;
(2)点Q关于直线AC的对称点为M,分别联结AM、PM;
①当点P分别在点Q左侧和右侧时,依据题意将图2、图3补全(不写画法);
②小明提出这样的猜想:点P、Q在运动的过程中,始终有PA=PM.经过小红验证,这个猜想是正确的,请你在①的点P、Q的两种位置关系中选择一种说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探寻“勾股数”:直角三角形三边长是整数时我们称之为“勾股数”,勾股数有多少?勾股数有规律吗?
(1)请你写出两组勾股数.
(2)试构造勾股数.构造勾股数就是要寻找3个正整数,使他们满足“两个数的平方和(或差)等于第三数的平方”,即满足以下形式:
① 2+ 2= 2;或② 2﹣ 2= 2
③要满足以上①、②的形式,不妨从乘法公式入手.我们已经知道③(x+y)2﹣(x﹣y)2=4xy.如果等式③右边也能写成 2的形式,就能符合②的形式.
因此不妨设x=m2,y=n2,(m、n为任意正整数,m>n),请你写出含m、n的这三个勾股数并证明它们是勾股数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线![]() 上部分点的横坐标
上部分点的横坐标![]() , 纵坐标
, 纵坐标![]() 的对应值如下表:
的对应值如下表:
| … |
|
| 0 | 1 | 2 | … |
| … | 0 | 4 | 6 | 6 | 4 | … |
从上表可知,下列说法正确的是 .
①抛物线与![]() 轴的一个交点为
轴的一个交点为![]() ; ②抛物线与
; ②抛物线与![]() 轴的交点为
轴的交点为![]() ;
;
③抛物线的对称轴是:直线![]() ; ④在对称轴左侧
; ④在对称轴左侧![]() 随
随![]() 增大而增大.
增大而增大.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,分别以点A和点B为圆心,大于![]() AB的长为半径画弧,两弧相交于点M,N,作直线MN,交BC于点D,连接AD.若△ADC的周长为10,AB=7,则△ABC的周长为 .
AB的长为半径画弧,两弧相交于点M,N,作直线MN,交BC于点D,连接AD.若△ADC的周长为10,AB=7,则△ABC的周长为 .

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com