
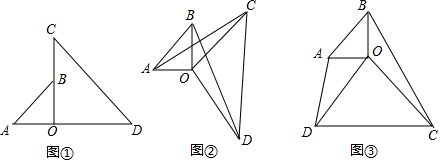
分析 (1)先由等腰直角三角形的性质判断出△AOC≌△BOD即可得出结论;
(2)同(1)的方法判断出∠ACO=∠BDO,再求出∠ACD+∠BDC=90°即可得出结论;
(3)利用中线构造出△BOE,则S△BOE=S△BOC,再证明△AOD≌△BOE,得S△BOE=S△AOD,即可.
解答 解:(1)如图①,连接AC,BD,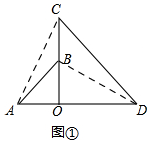
∵△AOB和△COD是两个都含有45°角的大小不同的直角三角板,
∴∠AOC=∠BOD=90°,OA=OB,OC=OD,
在△AOC和△BOD中,$\left\{\begin{array}{l}{OA=OB}\\{∠AOC=∠BOD=90°}\\{OC=OD}\end{array}\right.$,
∴△AOC≌△BOD,
∴AC=BD,
(2)如图②,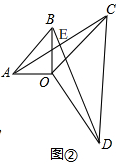 ∵△AOB和△COD是两个都含有45°角的大小不同的直角三角板,
∵△AOB和△COD是两个都含有45°角的大小不同的直角三角板,
∴OA=OB,OC=OD,∠AOB=∠COD=90°,
∴∠AOC=∠BOD
在△AOC和△BOD中,$\left\{\begin{array}{l}{OA=OB}\\{∠AOC=∠BOD}\\{OC=OD}\end{array}\right.$,
∴△AOC≌△BOD,
∴∠ACO=∠BDO,
∴∠ACD+∠BDC=∠ACO+∠OCD+(∠ODC-BDO)=∠OCD+∠ODC=90°,
∴∠CED=90°,
∴AC⊥BD;
(3)△AOD和△BOC面积相等,
理由:如图③,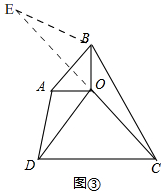
延长CO,在CO的延长线上取一点E,使OE=OC,
∵OC=OD,
∴OE=OD,
∵∠AOB=∠COD=90°,
∴∠AOD+∠BOC=180°,
∵∠BOE+∠BOC=180°,
∴∠BOE=∠AOD,
在△BOE和△AOD中,$\left\{\begin{array}{l}{BO=AO}\\{∠BOE=∠AOD}\\{OE=OD}\end{array}\right.$,
∴△BOE≌△AOD,
∴S△BOE=S△AOD,
∵OE=OC,
∴S△BOE=S△BOC,
∴S△AOD=S△BOC,
∴△AOD和△BOC面积相等.
点评 此题是几何变换综合题,主要考查了等腰直角三角形的性质,全等三角形的判定和性质,垂直的判断方法,三角形的中线分三角形面积相等的两部分,解本题的关键是判断出△AOC≌△BOD,是一道难度不大的中考常考题.


 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案科目:初中数学 来源: 题型:选择题
| A. | a+b | B. | abc | C. | 1000a+10b+c | D. | 100c+10b+a |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
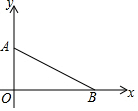 如图,点A的坐标为(0,1),点B的坐标为(2,0),若△ABC是等腰三角形,且点C在坐标轴上,则满足条件的点C有( )
如图,点A的坐标为(0,1),点B的坐标为(2,0),若△ABC是等腰三角形,且点C在坐标轴上,则满足条件的点C有( )| A. | 3个 | B. | 4个 | C. | 5个 | D. | 6个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
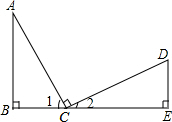 如图,Rt△ABC≌Rt△CED,点B、C、E在同一直线上,则结论:①AC=CD,②AC⊥CD,③BE=AB+DE,④AB∥ED,其中成立的有( )
如图,Rt△ABC≌Rt△CED,点B、C、E在同一直线上,则结论:①AC=CD,②AC⊥CD,③BE=AB+DE,④AB∥ED,其中成立的有( )| A. | 仅① | B. | 仅①③ | C. | 仅①③④ | D. | ①②③④ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com