
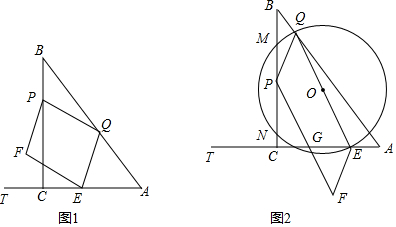
分析 (1)①如图1中,作QH⊥BC于H,QG⊥AC于G.,则四边形CGQH是矩形.在Rt△求出PH、QH即可解决问题.
②如图2中,连接PE交FQ于N,FQ交PC于G,作QM⊥AC于M.由四边形PQEF是平行四边形,推出PN=NE,由FQ∥AC,推出PG=GC,易证四边形CGQM是矩形,根据CG=QM,可得,解方程即可.
(2)分两种情形讨论①如图3中,连接PE,作FG⊥PC于G,QM⊥AC于M,PC交EF于H.②如图4中,作QG⊥BC于G,FM⊥AC于M,连接FQ,PF交AC于H.分别构建方程即可解决问题.
(3)如图5中,作OF⊥BC于F,OH⊥AC于H,FO的延长线交AB于T,CO的延长线交AB于K.由MN=EG,推出OF=OH,推出CK是∠ACB的平分线,易证:$\frac{AC}{BC}$=$\frac{AK}{BK}$,可得AK=$\frac{30}{7}$,由OT∥AE,QO=OE,推出QT=TA=m,由OT∥AC,由此列出方程即可解决问题.
解答 解:(1)①如图1中,作QH⊥BC于H,QG⊥AC于G.,则四边形CGQH是矩形.
在Rt△ABC,∵∠BCA=90°,BC=8,AB=10,
∴AC=$\sqrt{1{0}^{2}-{8}^{2}}$=6,
由题意CE=BP=2.5,AQ=5,
∵QG∥BC,
∴$\frac{QG}{BC}$=$\frac{AG}{AC}$=$\frac{AQ}{AB}$,
∴QG=4,AG=3,
∴CG=HQ=3,CH=GQ=4,PH=1.5,
∴PQ=PH2+QH2=1.52+32=$\frac{3}{2}\sqrt{5}$.
②如图2中,连接PE交FQ于N,FQ交PC于G,作QM⊥AC于M.
∵四边形PQEF是平行四边形,
∴PN=NE,
∵FQ∥AC,
∴PG=GC,
易证四边形CGQM是矩形,
CG=QM,
∴$\frac{1}{2}$(8-m)=$\frac{4}{5}$•2m,
∴m=$\frac{40}{21}$.
(2)①如图3中,连接PE,作FG⊥PC于G,QM⊥AC于M,PC交EF于H.
当H是EF中点时,S△PFH=$\frac{1}{2}$S△PEF,
∵S△PEF=S△PEQ,
∴?EQPF的面积恰好被线段BC分成1:3的两部分,
易证△FGH≌△ECH,△PFG≌△QEM,
∴FG=CE=EM,
∴m=6-m-$\frac{3}{5}$•2m,
∴m=$\frac{15}{8}$;
②如图4中,作QG⊥BC于G,FM⊥AC于M,连接FQ,PF交AC于H.
当PH=FH时,?EQPF的面积恰好被射线AT分成1:3的两部分,
易证FM=PC=PG,
∴8-m=m-$\frac{4}{5}$(10-2m),
∴m=$\frac{40}{7}$.
综上所述,当m=$\frac{15}{8}$或$\frac{40}{7}$时,?EQPF的面积恰好被线段BC或射线AT分成1:3的两部分.
(3)如图5中,作OF⊥BC于F,OH⊥AC于H,FO的延长线交AB于T,CO的延长线交AB于K.
∵MN=EG,
∴OF=OH,
∴CK是∠ACB的平分线,
易证:$\frac{AC}{BC}$=$\frac{AK}{BK}$,可得AK=$\frac{3}{7}$×10=$\frac{30}{7}$,
∵OT∥AE,QO=OE,
∴QT=TA=m,
∵OT∥AC,
∴$\frac{OT}{AC}$=$\frac{KT}{KA}$,
∴$\frac{\frac{1}{2}(6-m)}{6}$=$\frac{\frac{30}{7}-m}{\frac{30}{7}}$,
∴m=$\frac{10}{3}$,
∴m=$\frac{10}{3}$时,MN=EG.
故答案为$\frac{10}{3}$.
点评 本题考查圆综合题、平行四边形的性质、平行线分线段成比例定理、勾股定理、全等三角形的判定和性质等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,学会用方程的思想思考问题,属于中考压轴题.


 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案科目:初中数学 来源: 题型:选择题
| A. | 2x2+3x2=5x4 | B. | 2x2-3x2=-1 | C. | 2x2÷3x2=$\frac{2}{3}$x2 | D. | 2x2•3x2=6x4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
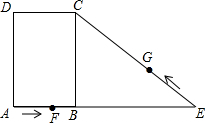 在矩形ABCD中,AB=4cm,AD=6cm,延长AB到E,使BE=2AB,连接CE,动点F从A出发以2cm/s的速度沿AE方向向点E运动,动点G从E点出发,以3cm/s的速度沿E→C→D方向向点D运动,两个动点同时出发,当其中一个动点到达终点时,另一个动点也随之停止,设动点运动的时间为t秒.
在矩形ABCD中,AB=4cm,AD=6cm,延长AB到E,使BE=2AB,连接CE,动点F从A出发以2cm/s的速度沿AE方向向点E运动,动点G从E点出发,以3cm/s的速度沿E→C→D方向向点D运动,两个动点同时出发,当其中一个动点到达终点时,另一个动点也随之停止,设动点运动的时间为t秒.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3.00909×104 | B. | 3.00909×105 | C. | 3.00909×1012 | D. | 3.00909×1013 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
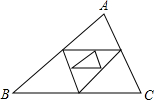 如下图,已知△ABC周长为1,连结△ABC三边的中点构成第二个三角形,再连结第二个三角形三边中点构成第三个三角形,依此类推,第2017个三角形周长为( )
如下图,已知△ABC周长为1,连结△ABC三边的中点构成第二个三角形,再连结第二个三角形三边中点构成第三个三角形,依此类推,第2017个三角形周长为( )| A. | $\frac{1}{2016}$ | B. | $\frac{1}{2017}$ | C. | $\frac{1}{{2}^{2016}}$ | D. | $\frac{1}{{2}^{2017}}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
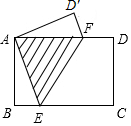 如图,矩形纸片ABCD中,AB=3cm,现将纸片折叠压平,使点A与点C重合,折痕为EF,如果sin∠BAE=$\frac{5}{13}$,那么重叠部分△AEF的面积为( )
如图,矩形纸片ABCD中,AB=3cm,现将纸片折叠压平,使点A与点C重合,折痕为EF,如果sin∠BAE=$\frac{5}{13}$,那么重叠部分△AEF的面积为( )| A. | $\frac{39}{4}$ | B. | $\frac{39}{8}$ | C. | $\frac{15}{4}$ | D. | $\frac{15}{8}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com