
【题目】如图.在等边△ABC中,AC=8,点D,E,F分别在三边AB,BC,AC上,且AF=2,FD⊥DE,∠DFE=60°,则AD的长为 . 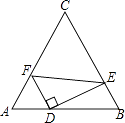
【答案】3
【解析】解:

∵∠DFE=60°,
∴∠1+∠2+60°=180°,
∴∠2=120°﹣∠1,
在等边△ABC中,∠A=∠C=60°,
∴∠A+∠1+∠3=180°,
∴∠3=180°﹣∠A﹣∠1=120°﹣∠1,
∴∠2=∠3,
又∵∠A=∠C,
∴△ADF∽△CFE,
∴ ![]() =
= ![]() ,
,
∵FD⊥DE,∠DFE=60°,
∴∠DEF=90°﹣60°=30°,
∴DF= ![]() EF,
EF,
又∵AF=2,AC=8,
∴CF=8﹣2=6,
∴ ![]() =
= ![]() ,
,
解得AD=3.
所以答案是:3.
【考点精析】解答此题的关键在于理解等边三角形的性质的相关知识,掌握等边三角形的三个角都相等并且每个角都是60°,以及对相似三角形的判定与性质的理解,了解相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方.


科目:初中数学 来源: 题型:
【题目】图1是一个长为2x、宽为2y的长方形,沿图中虚线用剪刀剪成四个完全相同的小长方形,然后按图2所示拼成一个正方形.
(1)你认为图2中的阴影部分的正方形的边长等于
(2)试用两种不同的方法求图2中阴影部分的面积.
方法1: 方法2:
(3)根据图2你能写出下列三个代数式之间的等量关系吗?
代数式:(x+y)2,(x-y)2,4xy.
(4)根据(3)题中的等量关系,解决如下问题:
若x+y=4,xy=3,则(x-y)2=
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O为平面直角坐标系的原点,点A在x轴上,△AOC是边长为2的等边三角形.
(1)写出△AOC的顶点C的坐标:_____.
(2)将△AOC沿x轴向右平移得到△OBD,则平移的距离是_____
(3)将△AOC绕原点O顺时针旋转得到△OBD,则旋转角可以是_____度
(4)连接AD,交OC于点E,求∠AEO的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)填空:
(a-b)(a+b)=________;
(a-b)(a2+ab+b2)=________;
(a-b)(a3+a2b+ab2+b3)=________;
(2)猜想:
(a-b)(an-1+an-2b+an-3b2+…+abn-2+bn-1)=________(其中n为正整数,且n≥2);
(3)利用(2)猜想的结论计算:
①29+28+27+…+22+2+1;
②210-29+28-…-23+22-2.
查看答案和解析>>
科目:初中数学 来源: 题型:
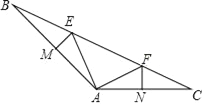
【题目】如图,已知△ABC中∠BAC=135°,点E,点F在BC上,EM垂直平分AB交AB于点M,FN垂直平分AC交AC于点N,BE=12,CF=9.
(1)判断△EAF的形状,并说明理由;
(2)求△EAF的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】永州市是一个降水丰富的地区,今年4月初,某地连续降雨导致该地某水库水位持续上涨,下表是该水库4月1日~4月4日的水位变化情况:
日期x | 1 | 2 | 3 | 4 |
水位y(米) | 20.00 | 20.50 | 21.00 | 21.50 |
(1)请建立该水库水位y与日期x之间的函数模型;
(2)请用求出的函数表达式预测该水库今年4月6日的水位;
(3)你能用求出的函数表达式预测该水库今年12月1日的水位吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《算法统宗》是中国古代数学名著,作者是我国明代数学家程大位.在《算法统宗》中记载:“以绳测井,若将绳三折测之,绳多4尺,若将绳四折测之,绳多1尺,绳长井深各几何?”
译文:“用绳子测水井深度,如果将绳子折成三等份,井外余绳4尺;如果将绳子折成四等份,井外余绳1尺.问绳长、井深各是多少尺?”
设井深为x尺,根据题意列方程,正确的是( )

A. 3(x+4)=4(x+1) B. 3x+4=4x+1
C. 3(x﹣4)=4(x﹣1) D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,∠A=90°,AD∥BC,E为AB的中点,连接CE,BD,过点E作FE⊥CE于点E,交AD于点F,连接CF,已知2AD=AB=BC.
(1)求证:CE=BD;
(2)若AB=4,求AF的长度;
(3)求sin∠EFC的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com