
| 3 | 4 |
| CD |
| AD |
| 3 |
| 4 |
| OG |
| CD |
| BO |
| BD |
| 1 |
| 2 |
| BG |
| GC |
| BO |
| OD |
| 1 |
| 1 |
| 1 |
| 2 |
| CF |
| OG |
| CE |
| EG |
| CF |
| 3 |
| 5 |
| 5+4 |
| 5 |
| 3 |
| DE2-DC2 |
| 82-62 |
| 7 |
| BE |
| AD |
| BP |
| PD |
8+2
| ||
| 8 |
4+
| ||
| 4 |
| 7 |
| 7 |
10(8-
| ||
| 57 |
40(8-
| ||
| 57 |
320-40
| ||
| 57 |
| BP |
| PD |
| BE |
| AD |
8-2
| ||
| 8 |
4-
| ||
| 4 |
| 7 |
10(8+
| ||
| 57 |
40(8+
| ||
| 57 |
320+40
| ||
| 57 |
| 1 |
| 2 |
| BP |
| BD |
| 1 |
| 3 |
| BP |
| 10 |
| 1 |
| 3 |
| 10 |
| 3 |
| 20 |
| 3 |
| 82-62 |
| 7 |
| BE |
| AD |
| ||
| 4 |
| BP |
| PD |
|
160-40
| ||
| 9 |
320-40
| ||
| 57 |
320+40
| ||
| 57 |
| 20 |
| 3 |
160-40
| ||
| 9 |


 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案科目:初中数学 来源: 题型:
| ∠BEO | ∠BOF |
查看答案和解析>>
科目:初中数学 来源:中学学习一本通 数学 七年级下册 北师大课标 题型:022
| |||||||||||||||
查看答案和解析>>
科目:初中数学 来源:2013年上海市中考数学试卷(试运转)(解析版) 题型:解答题
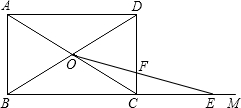
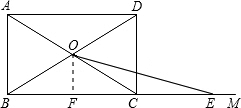
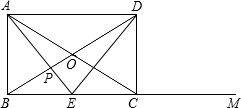
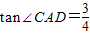 ,对角线AC与BD相交于O点.在射线BM上截取一点E,使OC=CE,连接OE,与边CD相交于点F.
,对角线AC与BD相交于O点.在射线BM上截取一点E,使OC=CE,连接OE,与边CD相交于点F.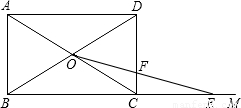
查看答案和解析>>
科目:初中数学 来源:2011年上海市初中毕业生统一学业考试数学试卷(试运转)(解析版) 题型:解答题
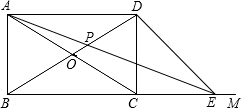
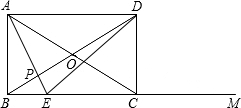
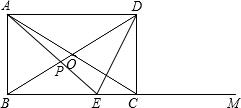
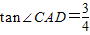 ,对角线AC与BD相交于O点.在射线BM上截取一点E,使OC=CE,连接OE,与边CD相交于点F.
,对角线AC与BD相交于O点.在射线BM上截取一点E,使OC=CE,连接OE,与边CD相交于点F.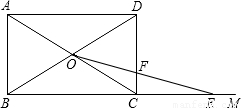
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com