
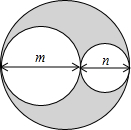
 三个圆的位置如图所示,m,n分别是两个较小的圆的直径,m+n是最大圆的直径,则图中阴影部分的面积为( )
三个圆的位置如图所示,m,n分别是两个较小的圆的直径,m+n是最大圆的直径,则图中阴影部分的面积为( )| A. | 2πmn | B. | $\frac{1}{2}$πmn | C. | π(m+n) | D. | πmn |
分析 由图知:阴影部分的面积等于以(m+n)为直径的圆的面积减去两个分别以m、n为直径的小圆的面积.
解答 解:若以(m+n)、m、n为直径的圆分别用S圆(m+n)、S圆m、S圆n表示.
由图知:S阴影=S圆(m+n)-S圆m-S圆n
=π×($\frac{m+n}{2}$)2-π×($\frac{m}{2}$)2-π×($\frac{n}{2}$)2
=$\frac{π}{4}$×(m+n)2-$\frac{π}{4}$×m2-$\frac{π}{4}×{n}^{2}$
=$\frac{π}{4}$[(m+n)2-m2-n2]
=$\frac{π}{4}$×2mn
=$\frac{1}{2}$πmn.
故选B.
点评 本题主要考查了整式的混合运算,发现阴影部分的面积与三个圆面积之间的关系是解决本题的关键.圆的面积公式:S圆=πr2(r为圆的半径).


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | 0.8 | C. | 0.6 | D. | 0.4 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在△PAB中,PA=PB,M,N,K分别是PA,PB,AB上的点,且AM=BK,BN=AK,若∠MKN=40°,则∠P的度数为( )
如图,在△PAB中,PA=PB,M,N,K分别是PA,PB,AB上的点,且AM=BK,BN=AK,若∠MKN=40°,则∠P的度数为( )| A. | 100° | B. | 110° | C. | 80° | D. | 90° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
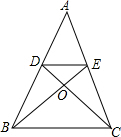 如图,△ABC中,DE∥BC,$\frac{AD}{BD}$=$\frac{1}{2}$,则OE:OB=( )
如图,△ABC中,DE∥BC,$\frac{AD}{BD}$=$\frac{1}{2}$,则OE:OB=( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com