
【题目】如图,抛物线y=﹣x2+bx+c与x轴交于A、B两点,与y轴交于点C,点O为坐标原点,点D为抛物线的顶点,点E在抛物线上,点F在x轴上,四边形OCEF为矩形,且OF=2,EF=3,

(1)求抛物线所对应的函数解析式;
(2)求△ABD的面积;
(3)将△AOC绕点C逆时针旋转90°,点A对应点为点G,问点G是否在该抛物线上?请说明理由.
【答案】(1)抛物线所对应的函数解析式为y=﹣x2+2x+3;
(2)△ABD的面积=![]() ×4×4=8;
×4×4=8;
(3)点G不在该抛物线上,理由见解析.
【解析】
试题分析:(1)在矩形OCEF中,已知OF、EF的长,先表示出C、E的坐标,然后利用待定系数法确定该函数的解析式.
(2)根据(1)的函数解析式求出A、B、D三点的坐标,以AB为底、D点纵坐标的绝对值为高,可求出△ABD的面积.
(3)首先根据旋转条件求出G点的坐标,然后将点G的坐标代入抛物线的解析式中直接进行判定即可.
解:(1)∵四边形OCEF为矩形,OF=2,EF=3,
∴点C的坐标为(0,3),点E的坐标为(2,3).
把x=0,y=3;x=2,y=3分别代入y=﹣x2+bx+c中,
得![]() ,
,
解得![]() ,
,
∴抛物线所对应的函数解析式为y=﹣x2+2x+3;
(2)∵y=﹣x2+2x+3=﹣(x﹣1)2+4,
∴抛物线的顶点坐标为D(1,4),
∴△ABD中AB边的高为4,
令y=0,得﹣x2+2x+3=0,
解得x1=﹣1,x2=3,
所以AB=3﹣(﹣1)=4,
∴△ABD的面积=![]() ×4×4=8;
×4×4=8;
(3)△AOC绕点C逆时针旋转90°,CO落在CE所在的直线上,由(2)可知OA=1,
∴点A对应点G的坐标为(3,2),
当x=3时,y=﹣32+2×3+3=0≠2,所以点G不在该抛物线上.


 活力课时同步练习册系列答案
活力课时同步练习册系列答案科目:初中数学 来源: 题型:
【题目】某小区准备新建50个停车位,以解决小区停车难的问题.已知新建1个地上停车位和1个地下停车位共需0.5万元;新建3个地上停车位和2个地下停车位共需1.1万元.
(1)该小区新建1个地上停车位和1个地下停车位各需多少万元?
(2)若该小区预计投资金额超过10万元,且地上的停车位要求不少于30个,问共有几种建造方案?
(3)对(2)中的几种建造方案中,哪一个方案的投资最少?并求出最少投资金额.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,三角形ABC在直角坐标系中,
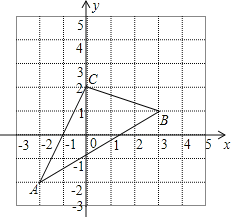
(1)若把△ABC向上平移2个单位,再向左平移1个单位得到△A′B′C′,请在图中画出平移后图形.
(2)请写出△A′B′C′各点的坐标.
(3)求出三角形ABC的面积._________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班开展1分钟仰卧起坐比赛活动,5名同学的成绩如下(单位:个):37、38、40、40、42.这组数据的众数是( )
A. 37 B. 38 C. 40 D. 42
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“把弯曲的公路改直,就能缩短路程”,其中蕴含的数学道理是( )
A. 两点确定一条直线 B. 直线比曲线短
C. 两点之间直线最短 D. 两点之间线段最短
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小颖和小亮上山游玩,小颖乘坐缆车,小亮步行,两人相约在山顶的缆车终点会合.已知小亮行走到缆车终点的路程是缆车到山顶的线路长的2倍,小颖在小亮出发后50 分钟才乘上缆车,缆车的平均速度为180 米/分钟.设小亮出发x 分钟后行走的路程为y m.图中的折线表示小亮在整个行走过程中y与x的函数关系.
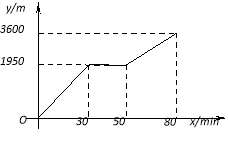
(1)小亮行走的总路程是____________㎝,他途中休息了________min.
(2)①当50≤x≤80时,求y与x的函数关系式;
②当小颖到达缆车终点为时,小亮离缆车终点的路程是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com