
数学与生产实际紧密联系,经常用于军事和国防上的计算.如图是设在我国某段海防线上的两个观测站A、B,上午9点,发现海面上C处有一可疑船只,通过通讯联络,立刻测得船只在观测站A的北偏东45°方向,在观测站B的北偏东30°的方向上,已知A、B两站的距离是50米,请你求出此时可疑船只离海岸线的距离(精确到米).(参考数据:![]() ≈1.73,
≈1.73,![]() ≈1.41)
≈1.41)

科目:初中数学 来源: 题型:
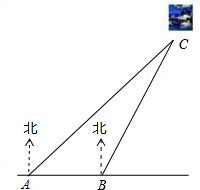 数学与生产实际紧密联系,经常用于军事和国防上的计算.如图是设在我国某段海防线上的两个观测站A、B,上午9点,发现海面上C处有一可疑船只,通过通讯联络,立刻测得船只在观测站A的北偏东45°方向,在观测站B的北偏东30°的方向上,已知A、B两站的距离是50米,请你求出此时可疑船只离海岸线的距离(精确到米).(参考数据:
数学与生产实际紧密联系,经常用于军事和国防上的计算.如图是设在我国某段海防线上的两个观测站A、B,上午9点,发现海面上C处有一可疑船只,通过通讯联络,立刻测得船只在观测站A的北偏东45°方向,在观测站B的北偏东30°的方向上,已知A、B两站的距离是50米,请你求出此时可疑船只离海岸线的距离(精确到米).(参考数据:| 3 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
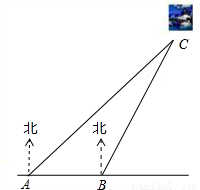
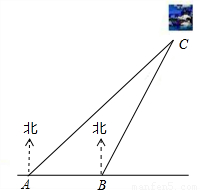
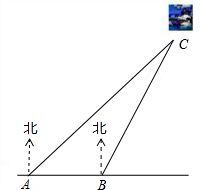 数学与生产实际紧密联系,经常用于军事和国防上的计算.如图是设在我国某段海防线上的两个观测站A、B,上午9点,发现海面上C处有一可疑船只,通过通讯联络,立刻测得船只在观测站A的北偏东45°方向,在观测站B的北偏东30°的方向上,已知A、B两站的距离是50米,请你求出此时可疑船只离海岸线的距离(精确到米).(参考数据:
数学与生产实际紧密联系,经常用于军事和国防上的计算.如图是设在我国某段海防线上的两个观测站A、B,上午9点,发现海面上C处有一可疑船只,通过通讯联络,立刻测得船只在观测站A的北偏东45°方向,在观测站B的北偏东30°的方向上,已知A、B两站的距离是50米,请你求出此时可疑船只离海岸线的距离(精确到米).(参考数据: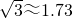 ,
,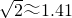 )
)查看答案和解析>>
科目:初中数学 来源:2012年广东省珠海市斗门区中考数学一模试卷(解析版) 题型:解答题
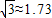 ,
,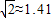 )
)
查看答案和解析>>
科目:初中数学 来源:2011年云南省玉溪市红塔区初中毕业数学试卷(解析版) 题型:解答题
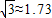 ,
,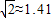 )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com