
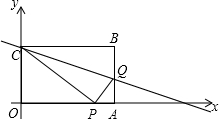
 如图,在平面直角坐标系中,矩形OABC的直角边OA、OC分别在x轴的正半轴和y轴的正半轴上,过点C的直线y=-$\frac{1}{3}$x+a交矩形的AB边于点Q,AQ=b.
如图,在平面直角坐标系中,矩形OABC的直角边OA、OC分别在x轴的正半轴和y轴的正半轴上,过点C的直线y=-$\frac{1}{3}$x+a交矩形的AB边于点Q,AQ=b.分析 (1)利用待定系数法即可得出结论;
(2)①先判断出△COP∽△PAQ,得出PA,最后用勾股定理建立方程即可得出结论;
②解法一、先求出点P,Q坐标,构造出圆,确定出圆心I的坐标,分两种情况讨论计算;
解法二、先求出∠QCP的正切值,再分三种情况讨论计算即可得出结论.
解答 解:(1)当y=b时,$b=-\frac{1}{3}x+a$,解得:x=3a-3b.
∴点Q的坐标为Q(3a-3b,b),
(2)①∵四边形OABC是矩形,
∴OA=CB=3a-3b
在$y=-\frac{1}{3}x+a$中,当x=0时,y=a,
∴AB=OC=a,又AQ=b,
∴BQ=a-b,
∵△BQC与△PQC关于CQ对称,
∴BQ=PQ=a-b,∠CPQ=∠B=90°,
∴∠OPC+∠APQ=90°
又∠OPC+∠OCP=90°,
∴∠APQ=∠OCP
又∠COP=∠PAQ=90°,
∴△COP∽△PAQ,
∴$\frac{CO}{PA}=\frac{CP}{PQ}$,$\frac{a}{PA}=\frac{3a-3b}{a-b}$,解得:$PA=\frac{a}{3}$.
在Rt△APQ中,由勾股定理得:PA2+AQ2=PQ2,
∴${({\frac{a}{3}})^2}+{b^2}={({a-b})^2}$,解得:$a=\frac{9}{4}b$.
②解法一:
如图1,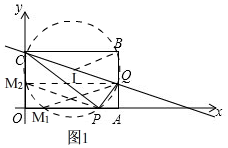 当b=4时,$a=\frac{9}{4}×4=9$,OA=CB=3a-3b=3×(9-4)=15,$PA=\frac{a}{3}=3$,OP=15-3=12,
当b=4时,$a=\frac{9}{4}×4=9$,OA=CB=3a-3b=3×(9-4)=15,$PA=\frac{a}{3}=3$,OP=15-3=12,
∴点Q(15,4),P(12,0).
取CQ的中点I,连接IB,
在Rt△CBQ中,$IB=\frac{1}{2}CQ$,
以点I为圆心,IB为半径作圆,
由轴对称性可知:点P在⊙I上,⊙I交x轴、y轴得异于C、P的点M1、M2,
连接M1Q、M2P、M2Q,
由同弧所对的圆周角相等可得:∠PM1Q=∠PM2Q=∠PCQ=∠QCB.
由(1)得Q的坐标为Q(3a-3b,b),BQ=a-b,
∴$tan∠QCB=\frac{BQ}{CB}=\frac{a-b}{3a-3b}=\frac{1}{3}$
∴$tan∠PCQ=tan∠QCB=\frac{1}{3}$.
由点C(0,9)与Q(15,4)可得中点I的坐标为$({\frac{15}{2},\;\frac{13}{2}})$.
分两种情况讨论:
当点M在x轴上时,即设点M1的坐标为(x,0),则IM1=IQ,
由勾股定理可得:${({\frac{15}{2}-x})^2}+{({\frac{13}{2}-0})^2}={({\frac{15}{2}-15})^2}+{({\frac{13}{2}-4})^2}$,解得:x1=3或x2=12(不合舍去),∴点M1(3,0).
∴点M1(3,0)关于点A(15,0)的对称点M4(27,0)也符合题意.
当点M在y轴上时,即设点M2的坐标为(0,y),则IM2=IQ,$IM_2^2=I{Q^2}$,
由勾股定理可得:${({\frac{15}{2}-0})^2}+{({\frac{13}{2}-y})^2}={({\frac{15}{2}-15})^2}+{({\frac{13}{2}-4})^2}$,解得:y1=9或y2=4,
∴点M2(0,4)、M3(0,9).
综上,点M的坐标为M1(3,0)、M2(0,4)、M3(0,9)、M4(27,0).
解法二:如图2,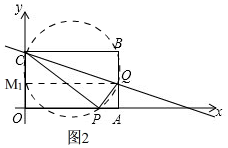 当b=4时,$a=\frac{9}{4}×4=9$,OA=CB=CP=3a-3b=15,PQ=BQ=a-b=5.
当b=4时,$a=\frac{9}{4}×4=9$,OA=CB=CP=3a-3b=15,PQ=BQ=a-b=5.
i)在Rt△CQP中,$tan∠QCP=\frac{PQ}{CP}=\frac{5}{15}=\frac{1}{3}$,
∴点C为符合题意的点,此时点C(0,9).
ii)作△CQP的外接圆交y轴得异于C点的点M1,连接M1Q,
∴∠QM1P=∠QCP
∵∠CM1P=∠CPQ=90°,∴M1Q⊥y轴,M1(0,4).
iii)在直线$y=-\frac{1}{3}x+9$中,令y=0,则x=27,
∴直线CQ与x轴的交点M4(27,0),
在Rt△QM4A中,$tan∠Q{M_4}A=\frac{QA}{{A{M_4}}}=\frac{4}{27-15}=\frac{1}{3}$,
∴点M4(27,0)是符合题意的点.
iv)点M4(27,0)是关于QA的对称点为点M3(3,0),此时∠QM3P=∠QM4A,
∴点M3(3,0)是符合题意的点.
综上,符合题意的点M的坐标为M1(0,9)、M2(0,4)、M3(3,0)、M4(27,0).
点评 此题是一次函数综合题,主要考查了待定系数法,相似三角形的判定和性质,勾股定理,对称的性质,解本题的关键是作出辅助线,分类讨论的思想.


 精英口算卡系列答案
精英口算卡系列答案科目:初中数学 来源: 题型:填空题
 点A在反比例函数y=$\frac{3}{x}$的图象上,过点A作AH⊥x轴于点H,连结OA,tan∠AOH=$\frac{1}{3}$.
点A在反比例函数y=$\frac{3}{x}$的图象上,过点A作AH⊥x轴于点H,连结OA,tan∠AOH=$\frac{1}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
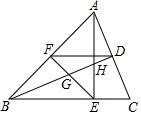 如图,在△ABC中,AE和BD是高,∠ABE=45°,点F是AB的中点,BD与FE,AE分别交于点G、H,∠CAE=∠ABD.有下列结论:①FD=FE;②BH=2CD;③BD•BH=2BE2;④S△ABC=$\frac{4}{3}$S四边形BCDF.其中正确的有( )
如图,在△ABC中,AE和BD是高,∠ABE=45°,点F是AB的中点,BD与FE,AE分别交于点G、H,∠CAE=∠ABD.有下列结论:①FD=FE;②BH=2CD;③BD•BH=2BE2;④S△ABC=$\frac{4}{3}$S四边形BCDF.其中正确的有( )| A. | ①③ | B. | ②④ | C. | ①②③ | D. | ①②④ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
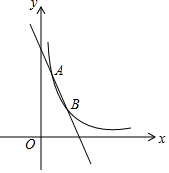 如图,一次函数y=kx+b与反比例函数y=$\frac{12}{x}$(x>0)的图象交于A(m,6),B(n,3)两点.
如图,一次函数y=kx+b与反比例函数y=$\frac{12}{x}$(x>0)的图象交于A(m,6),B(n,3)两点.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ①②③④ | B. | ①②④ | C. | ①②③ | D. | ①② |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com