
 设计一个商标图案如图中阴影部分所示,长方形ABCD中,AB=a,BC=b,以点A为圆心,AD为半径作圆弧与BA的延长线相交于点F,求商标图案的面积.(其中a=4,b=2).
设计一个商标图案如图中阴影部分所示,长方形ABCD中,AB=a,BC=b,以点A为圆心,AD为半径作圆弧与BA的延长线相交于点F,求商标图案的面积.(其中a=4,b=2). 分析 先利用扇形面积公式和三角形面积公式,得到商标图案的面积=$\frac{1}{4}$•π•b2+ab-$\frac{1}{2}$•(a+b)•b,然后去括号合并后把a和b的值代入计算即可.
解答 解:商标图案的面积=S扇形DAF+S矩形ABCD-S△FBC
=$\frac{1}{4}$•π•b2+ab-$\frac{1}{2}$•(a+b)•b
=($\frac{1}{4}$π-$\frac{1}{2}$)b2+$\frac{1}{2}$ab,
当a=4,b=2时,原式=(($\frac{1}{4}$π-$\frac{1}{2}$)•22+$\frac{1}{2}$•4•2=π+2.
点评 本题考查了整式的混合运算:有乘方、乘除的混合运算中,要按照先乘方后乘除的顺序运算,其运算顺序和有理数的混合运算顺序相似.解决本题的关键是利用扇形的面积、三角形和矩形的面积表示出阴影部分的面积.


科目:初中数学 来源: 题型:解答题
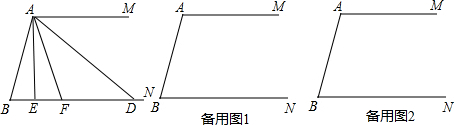
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
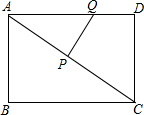 如图,矩形ABCD中,AB=6cm,BC=8cm,动点P从点A出发,在AC上以每秒5cm的速度向点C匀速运动,同时动点Q从点D出发,在DA边上以每秒4cm的速度向点A匀速运动,运动时间为t秒(0<t<2),连接PQ.
如图,矩形ABCD中,AB=6cm,BC=8cm,动点P从点A出发,在AC上以每秒5cm的速度向点C匀速运动,同时动点Q从点D出发,在DA边上以每秒4cm的速度向点A匀速运动,运动时间为t秒(0<t<2),连接PQ.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | k>0 | B. | k<0 | C. | k=0 | D. | 不能确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ①②③④ | B. | ②③④ | C. | ②④ | D. | ②③ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com