已知:点P是x轴负半轴上的一点,点A(4,0)在x轴上,点B在y轴的正半轴上,直线AB切⊙P于点D.⊙P的半径为15,AP与⊙P交于点C,PO-2OC=9.
求:(1)点P的坐标和AP的长;
(2)直线AB的函数解析式.
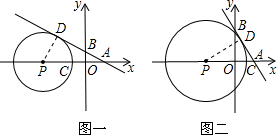
解:(1)当点C在线段PO上时,(如图一),
∵⊙P的半径为9,∴PC=15,∴PO-OC=15,
∵PO-2OC=9,∴PO=21,OC=6,
∴点P(-21,0)…
∵点A(4,0),∴AP=25.…
当点C在线段AO上时(如图二),
∵⊙P的半径为9,∴PC=15,∴PO+OC=15,
∵PO-2OC=9,∴PO=13,OC=2,
∴点P(-13,0)…
∵点A(4,0),∴AP=17.…
(2)当点C在线段PO上时,连接PD(如图一),
∵AB切⊙P于点D,∴PD⊥AD,PD=15.
∵AP=25,∴AD
2+PD
2=AP
2,∴AD=20. …
∵△ABO∽△APD,∴AO:AD=OB:PD,即4:20=OB:15,∴OB=3,…
∴可以求得切线AB的函数解析式为y=-

x+3. …
当点C在线段AO上时,连接PD(如图二),
∵AB切⊙P于点D,∴PD⊥AD,PD=15.
∵AP=17,∴AD
2+PD
2=AP
2,∴AD=8.…
∵△ABO∽△APD,
∵△ABO∽△APD,∴AO:AD=OB:PD,即4:8=OB:15,∴OB=
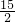
,…
∴可以求得切线AB的函数解析式为y=-
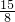
x+
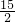
. …
分析:(1)当点C在线段PO上时(如图一),有PO-OC=PC=15,且PO-2OC=9,解方程组可求PO,从而确定点P的坐标和AP的长,当点C在线段AO上时(如图二),有PO+OC=PC=15,且PO-2OC=9,解方程组可求PO,从而确定点P的坐标和AP的长;
(2)根据(1)的两种情况,连接PD,分别在Rt△APD中,由勾股定理求AD,由△ABO∽△APD,利用相似比求OB,确定B点坐标,根据A、B两点坐标求直线AB的解析式.
点评:本题考查了一次函数的综合运用.关键是点C的位置分类,由勾股定理,相似三角形求B点坐标,确定直线AB的解析式.

 解:(1)当点C在线段PO上时,(如图一),
解:(1)当点C在线段PO上时,(如图一), x+3. …
x+3. …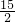 ,…
,…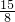 x+
x+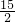 . …
. …