
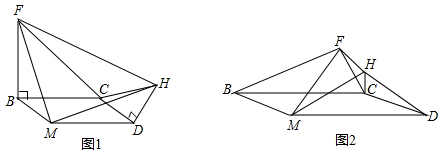
分析 (1)如图1中,延长BC交HM于N,FM交BC于O.只要证明△FBM≌△MDH即可解决问题;
(2)结论:∠FMH=α.如图1中,延长BC交HM于N,FM交BC于O.只要证明△FBM≌△MDH即可解决问题;
解答 (1)证明:如图1中,延长BC交HM于N,FM交BC于O.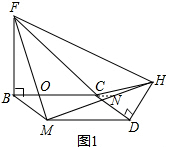
∵四边形BMDC是平行四边形,
∴BC=DM,BM=CD∠CBM=∠MDC,BC∥DM,
∵BF=BC,DC=DH,∠FBC=∠CDH=90°,
∴BF=DM,∠FBM=∠MDH,BM=DH,
∴△FBM≌△MDH,
∴FM=MH,∠BFM=∠DMH,
∵∠DMH=∠MNO,
∴∠OFB=∠ONM,
∵∠FOB=∠MON,
∴∠OMN=∠OBF=90°,
∴△FMH是等腰直角三角形.
(2)解:结论:∠FMH=α.
理由:如图1中,延长BC交HM于N,FM交BC于O.
∵四边形BMDC是平行四边形,
∴BC=DM,BM=CD∠CBM=∠MDC,BC∥DM,
∵BF=BC,DC=DH,∠FBC=∠CDH,
∴BF=DM,∠FBM=∠MDH,BM=DH,
∴△FBM≌△MDH,
∴∠BFM=∠DMH,
∵∠DMH=∠MNO,
∴∠OFB=∠ONM,
∵∠FOB=∠MON,
∴∠OMN=∠OBF,
∴∠FMH=α.
点评 本题考查平行四边形的性质、等腰直角三角形的性质、全等三角形的判定和性质等知识,解题的关键是正确寻找全等三角形解决问题,属于中考常考题型.


科目:初中数学 来源: 题型:解答题
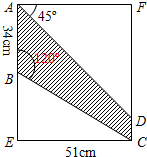 在2016首届合肥风筝文化节期间,某校丁周同学想在一个矩形材料中剪出如图阴影所示的图形,作为要制作的风筝的一个翅膀,请你根据图中的数据帮丁周同学计算出BE、CD的长度(精确到个位,$\sqrt{3}$≈1.7).
在2016首届合肥风筝文化节期间,某校丁周同学想在一个矩形材料中剪出如图阴影所示的图形,作为要制作的风筝的一个翅膀,请你根据图中的数据帮丁周同学计算出BE、CD的长度(精确到个位,$\sqrt{3}$≈1.7).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
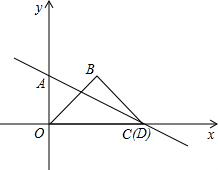 如图,在平面直角坐标系xOy中,已知直线AC的解析式为y=-$\frac{1}{4}$x+1,直线AC交x轴于点C,交y轴于点A.
如图,在平面直角坐标系xOy中,已知直线AC的解析式为y=-$\frac{1}{4}$x+1,直线AC交x轴于点C,交y轴于点A.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,△ABC在网格中(每格表示1个单位),如图所示构建平面直角坐标系
如图,△ABC在网格中(每格表示1个单位),如图所示构建平面直角坐标系查看答案和解析>>
科目:初中数学 来源: 题型:解答题
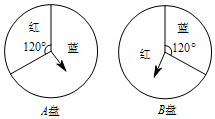 小明和小丽用如图所示的两个转盘做“配紫色”游戏:分别转动两个转盘,其中一个转盘转到红色,另一个转盘转到蓝色,即可配成紫色,两人商定,若能配成紫色,小明胜,否则小丽胜,这个游戏对双方公平吗?请说明理由.
小明和小丽用如图所示的两个转盘做“配紫色”游戏:分别转动两个转盘,其中一个转盘转到红色,另一个转盘转到蓝色,即可配成紫色,两人商定,若能配成紫色,小明胜,否则小丽胜,这个游戏对双方公平吗?请说明理由.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com