
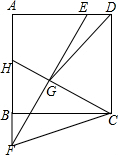
 如图,正方形ABCD中,AB=8$\sqrt{5}$,E是AD边上一点,F是AB延长线上一点,且DE=BF,连接EF,G是EF的中点,延长CG交AB于点H,H恰好是AB的中点,连接DG,则DG的长是多少?
如图,正方形ABCD中,AB=8$\sqrt{5}$,E是AD边上一点,F是AB延长线上一点,且DE=BF,连接EF,G是EF的中点,延长CG交AB于点H,H恰好是AB的中点,连接DG,则DG的长是多少? 分析 如图,连接EC,设EF交BC于O,作GM⊥AD于M,交BC于N,作GK⊥CD于K,交AB于L.首先证明△ECF是等腰直角三角形,四边形MDKG,四边形BNGL都是正方形,
再证明△GLH≌△GNO,推出GH=GO,由△GOC∽△BHC,可得$\frac{GC}{OG}$=$\frac{BC}{BH}$由BH=HA,推出$\frac{GC}{OG}$=$\frac{BC}{BH}$=2,由GN∥BH,推出$\frac{CG}{GH}$=$\frac{CN}{BN}$=2,推出GK=DK=CN=$\frac{2}{3}$BC=$\frac{16\sqrt{5}}{3}$,再利用等腰直角三角形的性质:DG=$\sqrt{2}$GK,即可解决问题.
解答 解:如图,连接EC,设EF交BC于O,作GM⊥AD于M,交BC于N,作GK⊥CD于K,交AB于L.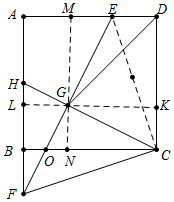
∵四边形ABCD是正方形,
∴AB=BC=CD=AD,∠ABC=∠ADC=∠BCD=∠A=90°,
∵DE=BF,
∴△CDE≌△CBF,
∴CE=CF,∠ECD=∠BCF,
∴∠ECF=∠DCB=90°,
∵EG=GF,
∴CG=GE=GF,CG⊥EF,
易知四边形AMGL,四边形MGKD,四边形GKCN,四边形BNGL是矩形,
∴∠MGK=∠EGC=90°,
∴∠MGE=∠KGC,∵∠GME=∠GKC=90°,
∴△GME≌△GKC,
∴GM=GK,
∴四边形MDKG是正方形,
∵KL=MN,
∴GL=GN,
∴四边形BNGL是正方形,
∵∠HGO=∠LGN=90°,
∴∠LGH=∠OGN,∵∠GLH=∠GNO=90°,
∴△GLH≌△GNO,
∴GH=GO,
∵△GOC∽△BHC,
∴$\frac{GC}{OG}$=$\frac{BC}{BH}$,∵BH=HA,
∴$\frac{GC}{OG}$=$\frac{BC}{BH}$=2,
∵GN∥BH,
∴$\frac{CG}{GH}$=$\frac{CN}{BN}$=2,
∴GK=DK=CN=$\frac{2}{3}$BC=$\frac{16\sqrt{5}}{3}$,
∴DG=$\sqrt{2}$GK=$\frac{16\sqrt{10}}{3}$.
点评 本题考查正方形的性质和判定、全等三角形的判定和性质、相似三角形的判定和性质、等腰直角三角形的性质、平行线分线段成比例定理等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com