A
分析:由勾股定理求出AB=10,连接FP、PE,过P作PM⊥AC于M,根据切线的性质得出矩形CMPF,推出PM=CF,PF=CM,设圆P的半径是r,根据切线的性质和切线长定理、等腰三角形的性质得到DF=FP,AM=PM,BE=BF,根据勾股定理得出AP
2=AE
2+PE
2=AM
2+PM
2,代入即可得到方程,求出方程的解即可.
解答:
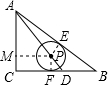
解:由勾股定理得:AB=

=10,
连接FP、PE,过P作PM⊥AC于M,
∵∠C=90°,PF⊥BC,
∴四边形CMPF是矩形,
∴PM=CF,PF=CM,
设圆P的半径是r,
∵AC=CD,∠C=90°,
∴∠ADC=45°,
∵PF⊥BC,
∴∠FPD=45°=∠ADC,
∴DF=FP=r,
同理:AM=PM,
∵圆P切AB于E,切BC于F,
∴BF=BE=BD+DF=8-6+r,
∴AE=10-(8-6+r)=8-r,
由勾股定理得:AP
2=AE
2+PE
2=AM
2+PM
2,
∴(6-r)
2+(6-r)
2=r
2+(8-r)
2,
解得:r=1,
故选A.
点评:本题主要考查对切线的性质,切线长定理,矩形的性质和判定,等腰三角形的性质和判定,勾股定理,直角三角形的性质,角平分线的定义,解一元一次方程等知识点的理解和掌握,题型较好,难度适中,综合性强.

 解:由勾股定理得:AB=
解:由勾股定理得:AB= =10,
=10,

 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案 导学教程高中新课标系列答案
导学教程高中新课标系列答案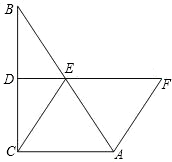 延长线上,且AF=CE.求证:四边形ACEF是菱形.
延长线上,且AF=CE.求证:四边形ACEF是菱形.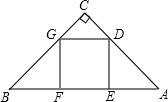 点G在边BC上.
点G在边BC上.