
【题目】如图,⊙O为Rt△ABC的内切圆,⊙O的半径r=1,∠B=30°,
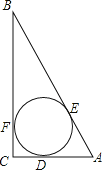
(1)劣弧DE的长.
(2)证明:AD=AE.
(3)求:劣弧DE、切线AD、AE所围成的面积S.
【答案】(1)![]() (2)证明见解析(3)
(2)证明见解析(3)![]() ﹣
﹣![]()
【解析】
试题分析:(1)根据切线的性质得出OD⊥AC,OE⊥AB,根据四边形内角和求得∠DOE=120°,代入公式求得即可;
(2)证得RT△AOD≌RT△AOE即可得到结论;
(3)根据S=S四边形ADOE﹣S扇形ODE求得即可.
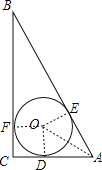
解:(1)连接OD、OE,则OD⊥A,COE⊥AB
∵∠B=30°∠C=90°
∴∠A=60°
∴∠DOE=120°
劣弧DE的长=![]() ;
;
(2)连接OA,
在RT△AOD和RT△AOE中
![]()
∴RT△AOD≌RT△AOE(HL),
∴AD=AE
(3)∵RT△AOD≌RT△AOE,
∴∠OAB=∠OAC=![]() ∠BAC=30°,
∠BAC=30°,
∴AE=![]() OE=
OE=![]() ,
,
∴四边形ADOE的面积=2×![]() AE
AE![]() OE=
OE=![]() ,
,
∵S扇形ODE=![]() =
=![]() π
π
∴S=S四边形ADOE﹣S扇形ODE=![]() ﹣
﹣![]() .
.


 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案科目:初中数学 来源: 题型:
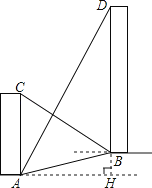
【题目】如图,AC、BD是一斜坡AB上的两幢楼房,斜坡AB的坡度是1:2![]() ,从点A测得楼BD顶部D处的仰角60°,从点B测得楼AC顶部C处的仰角30°,楼BD自身高度BD比楼AC高12米,求楼AC和楼BD之间的水平距离?(结果保留根号)
,从点A测得楼BD顶部D处的仰角60°,从点B测得楼AC顶部C处的仰角30°,楼BD自身高度BD比楼AC高12米,求楼AC和楼BD之间的水平距离?(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某车间有26名工人,每人每天可以生产800个螺钉或1000个螺母,1个螺钉需要配2个螺母,为使每天生产的螺钉和螺母刚好配套.设安排x名工人生产螺钉,则下面所列方程正确的是( )
A.2×1000(26﹣x)=800x B.1000(13﹣x)=800x
C.1000(26﹣x)=2×800x D.1000(26﹣x)=800x
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,抛物线y=﹣x2+2x+3与x轴交于A,B,与y轴交于C,抛物线的顶点为D,直线l过C交x轴于E(4,0).
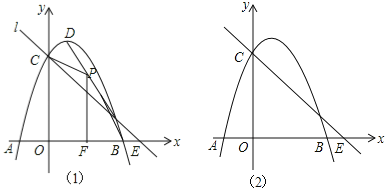
(1)写出D的坐标和直线l的解析式;
(2)P(x,y)是线段BD上的动点(不与B,D重合),PF⊥x轴于F,设四边形OFPC的面积为S,求S与x之间的函数关系式,并求S的最大值;
(3)点Q在x轴的正半轴上运动,过Q作y轴的平行线,交直线l于M,交抛物线于N,连接CN,将△CMN沿CN翻转,M的对应点为M′.在图2中探究:是否存在点Q,使得M′恰好落在y轴上?若存在,请求出Q的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com